Умение определять объем пространственных фигур является важным для решения геометрических и практических задач. Одной из таких фигур является призма. Рассмотрим в статье, что она собой представляет, и покажем, как вычислять объем наклонной призмы.
Что понимают под призмой в геометрии?
Речь идет о правильном полиэдре (многограннике), который образован двумя одинаковыми основаниями, находящимися в параллельных плоскостях, и несколькими параллелограммами, соединяющими отмеченные основания.
 Вам будет интересно:Албазинский острог: история основания
Вам будет интересно:Албазинский острог: история основания
Основаниями призмы могут быть произвольные многоугольники, например, треугольник, четырехугольник, семиугольник и так далее. Причем число углов (сторон) многоугольника определяет название фигуры.
Любая призма, имеющая в основании n-угольник (n - число сторон), состоит из n+2 граней, 2 × n вершин и 3 × n ребер. Из приведенных чисел видно, что количества элементов призмы соответствуют теореме Эйлера:
3 × n = 2 × n + n + 2 - 2
Ниже рисунок показывает, как выглядят треугольные и четырехугольные призмы, сделанные из стекла.
Виды фигуры. Наклонная призма
Выше уже было сказано, что название призмы определяется числом сторон многоугольника в основании. Однако существуют и другие особенности в ее строении, определяющие свойства фигуры. Так, если все параллелограммы, образующие боковую поверхность призмы, представлены прямоугольниками или квадратами, то такая фигура называется прямой. Для прямой призмы расстояние между основаниями равно длине бокового ребра любого прямоугольника.
Если же некоторые или все боковые стороны являются параллелограммами, то речь идет о наклонной призме. Высота ее уже будет меньше, чем длина бокового ребра.
Еще один критерий, по которому проводят классификацию рассматриваемых фигур — это длины сторон и углы многоугольника в основании. Если они равны друг другу, то многоугольник будет правильным. Прямая фигура с правильным многоугольником в основаниях называется правильной. С ней удобно работать при определении площади поверхности и объема. Наклонная призма в этом плане представляет некоторые трудности.
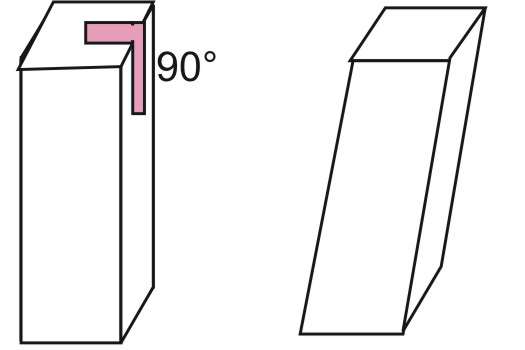
На приведенном рисунке показаны две призмы, имеющие четырехугольное основание. Угол 90° показывает принципиальную разницу между прямой и наклонной призмой.
Формула для определения объема фигуры
Часть пространства, ограниченная гранями призмы, называется ее объемом. Для рассматриваемых фигур любого типа эту величину можно определить по следующей формуле:
V = h × So
Здесь символом h обозначена высота призмы, которая является мерой дистанции между двумя основаниями. Символ So - одного основания площадь.
Площадь основания найти несложно. Учитывая тот факт, является правильным многоугольник или нет, а также зная количество его сторон, следует применить соответствующую формулу и получить So. Например, для правильного n-угольника с длиной стороны a площадь будет равна:
Sn = n / 4 × a2 × ctg (pi / n)
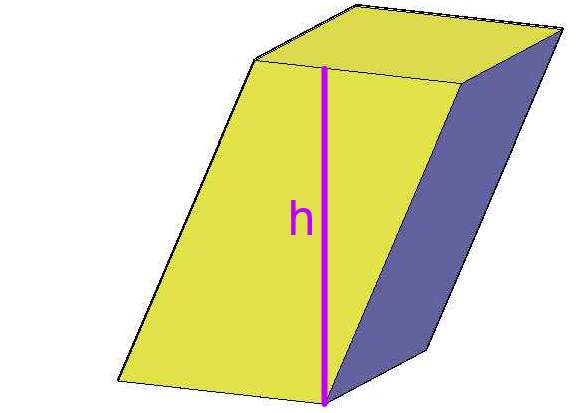
Теперь перейдем к высоте h. Для прямой призмы определение высоты не представляет никаких трудностей, однако для призмы наклонной - это непростая задача. Решать ее можно различными геометрическими методами, отталкиваясь от конкретных начальных условий. Тем не менее существует универсальный способ определения высоты фигуры. Опишем его кратко.
Идея заключается в нахождении расстояния от точки в пространстве до плоскости. Предположим, что плоскость задана уравнением:
A × x+ B × y + C × z + D = 0
Тогда от точки с координатами (x1; y1; z1) плоскость будет находиться на расстоянии:
h = |A × x1 + B × y1 + C × z1 + D| / √ (A2 + B2 + C2)
Если координатные оси расположить так, что точка (0; 0; 0) будет лежать в плоскости нижнего основания призмы, тогда уравнение для плоскости основания можно записать так:
z = 0
Это означает, что формула для высоты запишется так:
h = z1
Достаточно найти координату z любой точки верхнего основания, чтобы определить высоту фигуры.
Пример решения задачи
На рисунке ниже дана четырехугольная призма. Основанием наклонной призмы является квадрат со стороной 10 см. Необходимо вычислить ее объем, если известно, что длина бокового ребра равна 15 см, а острый угол фронтального параллелограмма равен 70°.
Поскольку высота h фигуры также является высотой параллелограмма, то используем формулы для определения его площади, чтобы найти h. Обозначим стороны параллелограмма так:
a = 10 см;
b = 15 см
Тогда можно записать для него следующие формулы для определения площади Sp:
Sp = a × b × sin (α);
Sp = a × h
Откуда получаем:
h = b × sin (α)
Здесь α - острый угол параллелограмма. Поскольку основанием является квадрат, то формула объема наклонной призмы примет вид:
V = a2 × b × sin (α)
Подставляем из условия данные в формулу и получаем ответ: V ≈ 1410 см3.

