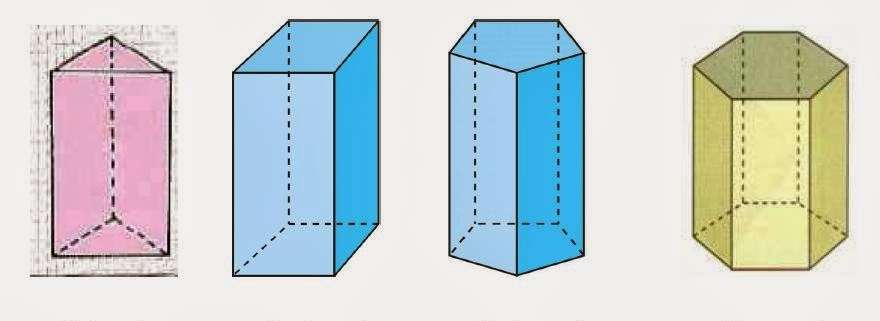
Стереометрия - раздел геометрии, изучающий фигуры, которые не лежат в одной плоскости. Одним из объектов изучения стереометрии являются призмы. В статье дадим определение призме с геометрической точки зрения, а также кратко перечислим свойства, которые для нее характерны.
Геометрическая фигура
Определение призмы в геометрии звучит следующим образом: это пространственная фигура, состоящая из двух одинаковых n-угольников, расположенных в параллельных плоскостях, соединенных друг с другом своими вершинами.
 Вам будет интересно:Круглый прямой цилиндр, развертка и формула для ее площади
Вам будет интересно:Круглый прямой цилиндр, развертка и формула для ее площади
Получить призму не представляет никакого труда. Представим, что есть два одинаковых n-угольника, где n - это число сторон или вершин. Поместим их так, чтобы они были друг другу параллельны. После этого вершины одного многоугольника следует соединить с соответствующими вершинами другого. Образованная фигура будет состоять из двух n-угольных сторон, которые называются основаниями, и n четырехугольных сторон, представляющих собой в общем случае параллелограммы. Совокупность параллелограммов образует боковую поверхность фигуры.
Существует еще один способ геометрического получения рассматриваемой фигуры. Так, если взять n-угольник и совершить его перенос в другую плоскость при помощи параллельных отрезков равной длины, то в новой плоскости мы получим исходный многоугольник. Оба многоугольника и все параллельные отрезки, проведенные из их вершин, образуют призму.
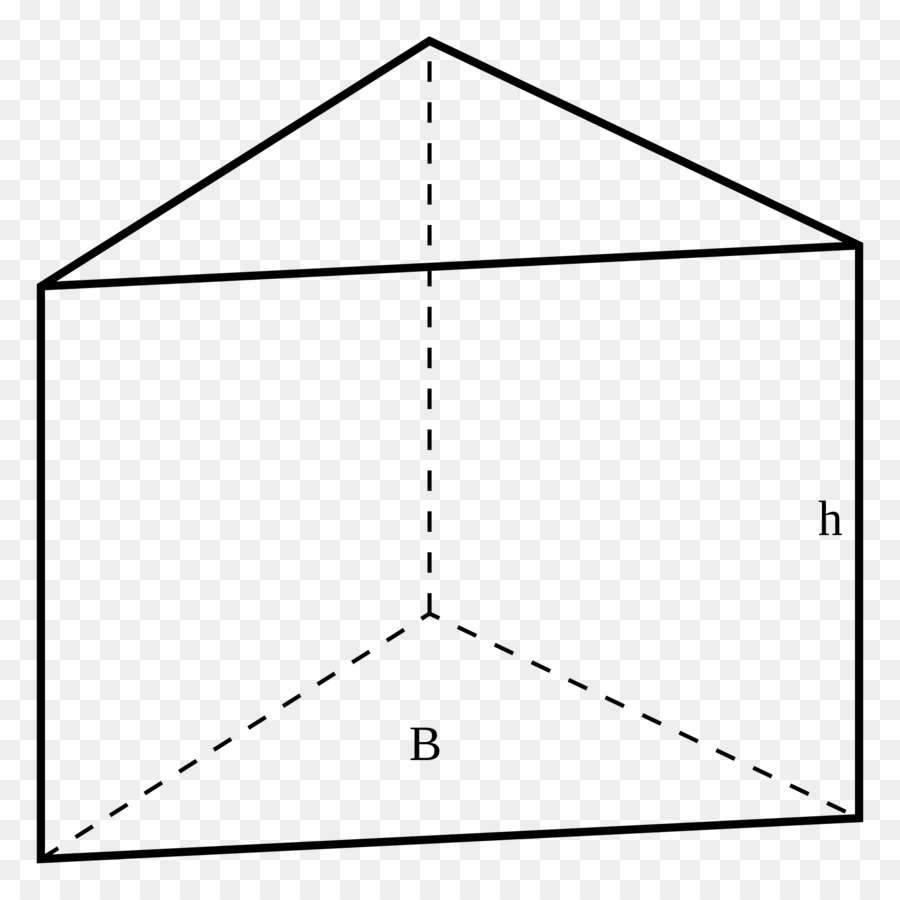
Рисунок выше демонстрирует треугольную призму. Так она называется потому, что ее основания представляют собой треугольники.
Элементы, из которых состоит фигура
Выше было дано определение призмы, из которого понятно, что главными элементами фигуры являются ее грани или стороны, ограничивающие все внутренние точки призмы от внешнего пространства. Любая грань рассматриваемой фигуры принадлежит к одному из двух типов:
- боковая;
- основания.
Боковых n штук, и они являются параллелограммами или их частными видами (прямоугольниками, квадратами). В общем случае боковые грани отличаются друг от друга. Граней основания всего две, они представляют собой n-угольники и друг другу равны. Таким образом, всякая призма имеет n+2 стороны.
Помимо сторон, фигура характеризуется своими вершинами. Они представляют собой точки, где соприкасаются одновременно три грани. Причем две из трех граней всегда принадлежат боковой поверхности, а одна - основанию. Таким образом, в призме нет специально выделенной одной вершины, как, например, в пирамиде, все они являются равноправными. Число вершин фигуры равно 2*n (по n штук для каждого основания).
Наконец, третьим важным элементом призмы являются ее ребра. Это отрезки определенной длины, которые образуются в результате пересечения сторон фигуры. Как и грани, ребра также имеют два разных типа:
- либо образованы только боковыми сторонами;
- либо возникают на стыке параллелограмма и стороны n-угольного основания.
Число ребер, таким образом, равно 3*n, причем 2*n из них относятся ко второму из названных типов.
Виды призм
Выделяют несколько способов классификации призм. Однако все они основаны на двух особенностях фигуры:
- на типе n-угольного основания;
- на типе боковой стороны.
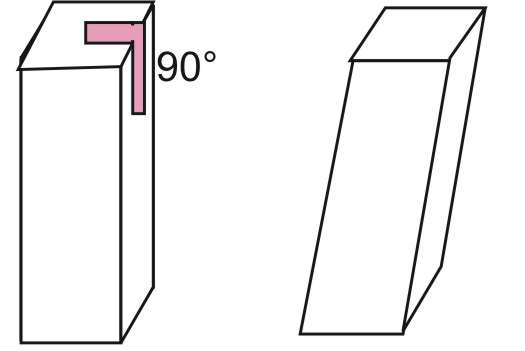
Для начала обратимся ко второй особенности и дадим определение призмы наклонной и прямой. Если хотя бы одна боковая сторона является параллелограммом общего типа, то фигура называется наклонной, или косоугольной. Если же все параллелограммы представляют собой прямоугольники или квадраты, то призма будет прямой.
Дать определение призмы прямой можно также несколько иначе: прямая фигура - это та призма, у которой боковые ребра и грани перпендикулярны ее основаниям. На рисунке показаны две четырехугольные фигуры. Левая является прямой, правая - наклонной.
Теперь перейдем к классификации согласно типу n-угольника, лежащего в основаниях. Он может иметь одинаковые стороны и углы или разные. В первом случае многоугольник называется правильным. Если рассматриваемая фигура содержит в основании многоугольник с равными сторонами и углами и является прямой, то она называется правильной. Согласно этому определению, правильная призма в основании может иметь равносторонний треугольник, квадрат, правильный пятиугольник или шестиугольник и так далее. Перечисленные правильные фигуры представлены на рисунке.
Линейные параметры призм
Для описания размеров рассматриваемых фигур используют следующие параметры:
- высота;
- стороны основания;
- длины боковых ребер;
- объемные диагонали;
- диагонали боковых сторон и оснований.
Для правильных призм все названные величины связаны друг с другом. Например, длины боковых ребер одинаковы и равны высоте. Для конкретной n-угольной правильной фигуры существуют формулы, позволяющие по двум любым линейным параметрам определить все остальные.
Поверхность фигуры
Если обратиться к данному выше определению призмы, то понять, что представляет поверхность фигуры, будет несложно. Поверхность - это площадь всех граней. Для прямой призмы она вычисляется по формуле:
S = 2*So + Po*h
где So - площадь основания, Po - периметр n-угольника в основании, h - высота (расстояние между основаниями).
Объем фигуры

Наряду с поверхностью для практики важно знать объем призмы. Определить его можно по следующей формуле:
V = So*h
Это выражение справедливо для абсолютно любого вида призм, включая те, которые являются наклонными и образованы неправильными многоугольниками.
Для правильных призм объем является функцией длины стороны основания и высоты фигуры. Для соответствующей n-угольной призмы формула для V имеет конкретный вид.