Вычисление площадей фигур является одной из приоритетных задач геометрии на плоскости и в пространстве. В данной статье рассмотрим объемную фигуру пирамиду. И покажем, какие формулы площади основания пирамиды следует применять для вычисления этой величины.
Что представляет собой пирамида?
Ответ на этот вопрос не столь очевиден, как многим может показаться. Когда люди слышат слово "пирамида", то в их воображении всплывает великое каменное сооружение египетских фараонов. Однако это лишь частный случай фигур этого класса.
 Вам будет интересно:Образ русской женщины в классической литературе
Вам будет интересно:Образ русской женщины в классической литературе
С точки зрения точной науки геометрии, пирамида является фигурой в пространстве, образованной n-угольником, каждая из вершин которого соединена с одной единственной точкой. Эта точка в плоскости n-угольника находиться не должна. Здесь n - целое число, равное количеству углов (сторон) плоского многоугольника. Для наглядного представления описанной фигуры приведем фотографию.

Здесь изображен набор самых разных пирамид. Верхняя левая называется треугольной, поскольку ее основание является треугольником. Нижняя правая пирамида называется двадцатиугольной.
Эта фотография позволяет сделать некоторые выводы, касающиеся пирамид. Во-первых, стороны, которые соединяют n-угольник с вершиной фигуры, представляют собой треугольники. Во-вторых, количество сторон любой пирамиды равно n+1 (один n-угольник и n треугольников), n-угольник называют основанием, а треугольники - боковыми гранями. В-третьих, можно заметить, что увеличение сторон основания приближает пирамиду по своей форме к конусу. Этот факт позволяет считать конус пирамидой с бесконечным числом боковых граней.
Правильные и неправильные фигуры
Мы выяснили, что такое основание фигуры. Тем не менее, до того как начать обсуждение формулы площади основания пирамиды, следует дать определение правильных и неправильных фигур этого класса.
Каждый школьник знает, что любой плоский многоугольник имеет геометрический центр. Если многоугольник изготовить из однородного материала, то геометрический центр совпадет с центром масс. Например, геометрический центр прямоугольника - это точка, где его диагонали пересекаются, для треугольника он находится в точке пересечения медиан. Концепция геометрического центра связана с понятиями правильной и неправильной пирамиды.
Выше было упомянуто о вершине пирамиды. Она соответствует точке, где пересекаются все треугольные боковые грани фигуры. Если из вершины опустить перпендикуляр к основанию, то длина полученного отрезка будет соответствовать расстоянию от вершины до основания. Этот отрезок называется высотой фигуры.
Если высота пересекает многоугольник в его геометрическом центре, то пирамида называется прямой. Если основанием прямой пирамиды будет многоугольник, имеющий стороны одинаковой длины и равные между собой углы, то пирамида называется правильной. Соответственно, если какое-либо из названных условий не выполняется, то говорят о неправильной пирамиде.

Согласно описанной классификации, пирамида Хеопса является правильной четырехугольной, имеющей в основании квадрат.
Площадь основания правильной пирамиды
Для вычисления площади основания пирамиды следует использовать соответствующие формулы для конкретного n-угольника. Например, в случае треугольника - это произведение высоты на основание, которое поделено пополам, в случае параллелограмма - это произведение стороны на опущенную на нее высоту.
Если n-угольник является правильным, то формула площади основания пирамиды будет универсальной. Запишем ее:
Sn = n/4*a2*ctg(pi/n)
Где параметр a - это длина стороны n-угольного основания. Эта формула справедлива независимо от того, рассматривается треугольная или стоугольная пирамида. Функцию котангенса следует вычислять с помощью калькулятора, однако для 3-, 4- и 6-угольника она имеет табличное значение.
Отметим, что данной формулой можно пользоваться, если основание пирамиды - это правильный многоугольник. Справедливость формулы не зависит от того, является пирамида прямой или наклонной.
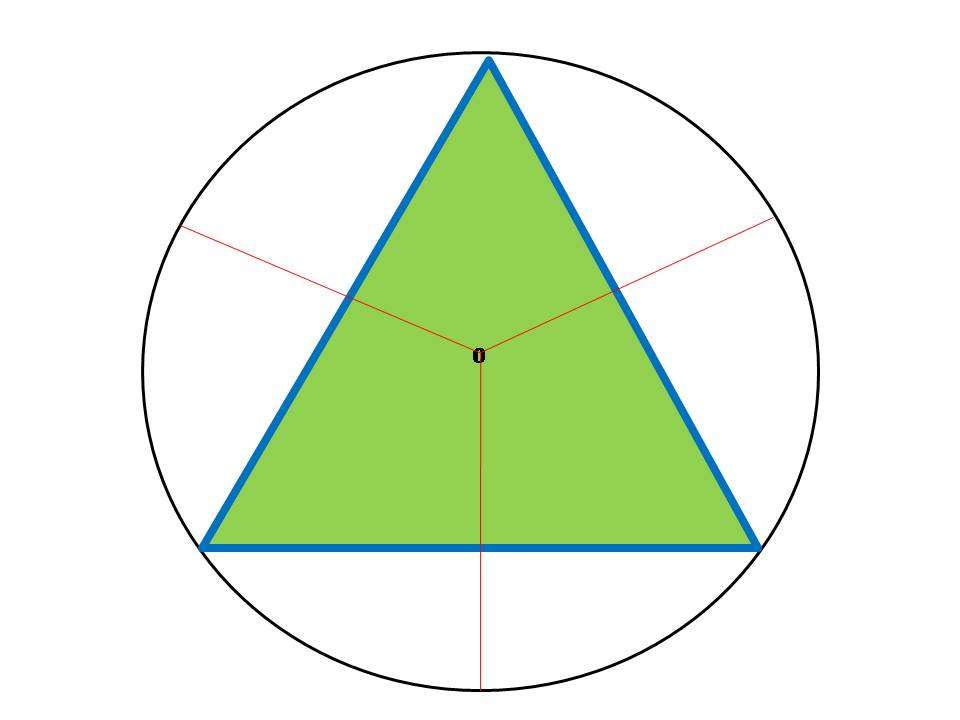
Пирамида треугольная правильная
Равносторонний треугольник является основанием правильной пирамиды треугольной. Площадь основания ее можно определить, если применить записанную в пункте выше формулу для Sn. Учитывая, что n = 3, получаем:
S3 = n/4*a2*ctg(pi/n) = 3/4*a2*ctg(pi/3) = √3/4*a2
Зная длину основания a, можно рассчитать соответствующую площадь.
Любопытно отметить, что в треугольной пирамиде, которую часто называют тетраэдром, все четыре стороны являются треугольниками. В правильной фигуре в общем случае только одна из сторон представляет собой равносторонний треугольник (основание). Остальные грани являются треугольниками равнобедренными.
Четырехугольная пирамида правильная

Пожалуй, она является самой знаменитой среди класса пирамид. Формула для площади основания пирамиды четырехугольной правильной известна школьнику уже в начальных классах, поскольку речь идет о площади квадрата. Следуя общему подходу, воспользуемся выражением для Sn. Подставляя n = 4, получаем:
S4 = 4/4*a2*ctg(pi/4) = a2
Например, найдем площадь основания четырехугольной пирамиды Хеопса. Длина стороны ее основания составляет приблизительно 230 метров. Это означает, что соответствующая площадь равна 52,9 тыс. м2, что больше площади 10 футбольных полей.
