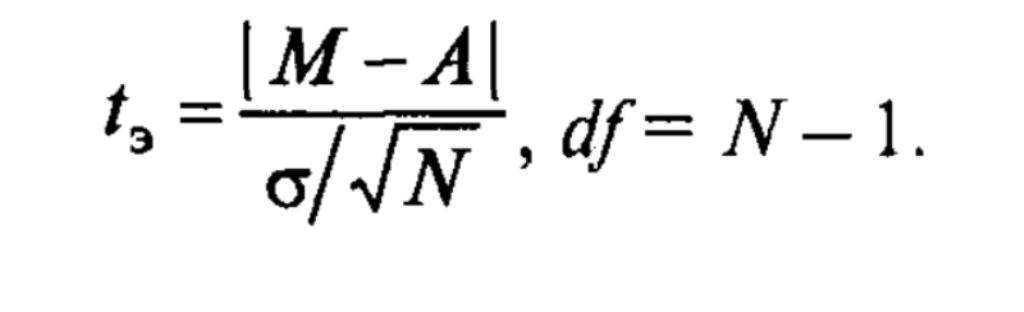Общий вопрос при сравнении двух наборов измерений заключается в том, следует ли использовать процедуру параметрического тестирования или непараметрическую. Чаще всего, используя симуляцию, сравнивают несколько параметрических и непараметрических тестов, таких как t-тест, нормальный тест (параметрические критерии), уровня Уилкоксона, оценки Ван-дер-Вальдена и т. д.(непараметрические).
Параметрические тесты предполагают базовые статистические распределения в данных. Поэтому необходимо выполнить несколько условий действительности, чтобы их результат был надежным. Непараметрические тесты не зависят от какого-либо распределения. Таким образом, они могут применяться, даже если параметрические условия действительности не выполняются. В данной статье мы рассмотрим параметрический метод, а именно - коэффициент корреляции Стьюдента.
Параметрический метод сравнения выборок (t-Стьюдента)
 Вам будет интересно:«Строете» или «строите»: как правильно?
Вам будет интересно:«Строете» или «строите»: как правильно?
Методы классифицируются на основе того, что мы знаем о субъектах, которых мы анализируем. Основная идея заключается в том, что существует набор фиксированных параметров, которые определяют вероятностную модель. Все виды коэффициента Стьюдента - это параметрические методы.
Ими часто являются те методы, при анализе которых мы видим, что субъект является приблизительно нормальным, поэтому перед тем, как использовать критерий, следует осуществить проверку на нормальность. То есть размещение признаков в таблице распределения Стьюдента (в обеих выборках) не должно существенно отличаться от нормального и обязано соответствовать или приблизительно согласовываться с указанным параметром. Для нормального распределения существует два показателя: среднее и стандартное отклонение.
Применение t критерия стьюдента производится при проверке гипотез. Он позволяет проверить допущение, применимое к испытуемым. Чаще всего этот критерий применяется для того, чтобы проверить, равны ли средние значения в двух выборках, но также может применяться и для одной.
Следует добавить, что преимущество использования параметрического теста вместо непараметрического состоит в том, что первое будет иметь большую статистическую мощность, чем последнее. Другими словами, параметрический тест более способен привести к отказу от нулевой гипотезы.
Критерии t-Стьюдента для одной выборки
Применение для одной выборки коэффициента Стьюдента - это статистическая процедура, используемая для определения того, может ли образец наблюдений быть создан процессом со специальным средним значением. Допустим, среднее значение рассматриваемого признака Mх отлично от определенного известного значения A. Это значит, что мы можем выдвинуть гипотезы H0 и H1. C помощью формулы t-эмпирического для одной выборки мы можем проверить какая из этих допущенных нами гипотез верна.
Формула эмпирического значения критерия t-Стьюдента:
Критерии t-Стьюдента для независимых выборок
Независимый коэффициент Стьюдента - это использование его, когда получаются два отдельных набора независимых и одинаково распределенных выборок, по одному от каждого из двух сравниваемых сопоставлений. При независимом допущении предполагается, что члены двух выборок не составят пары коррелирующих значений признака. Например, предположим, что мы оцениваем эффект медицинского лечения и зачисляем 100 пациентов в наше исследование, затем произвольно назначаем 50 пациентов в группу лечения и 50 - в контрольную. В этом случае мы имеем два независимых образца, соответственно, можем оформить статистические гипотезы H0 и H1 и проверить их с помощью данных нам формул.
Формулы для эмпирического значения критерия t-Стьюдента:
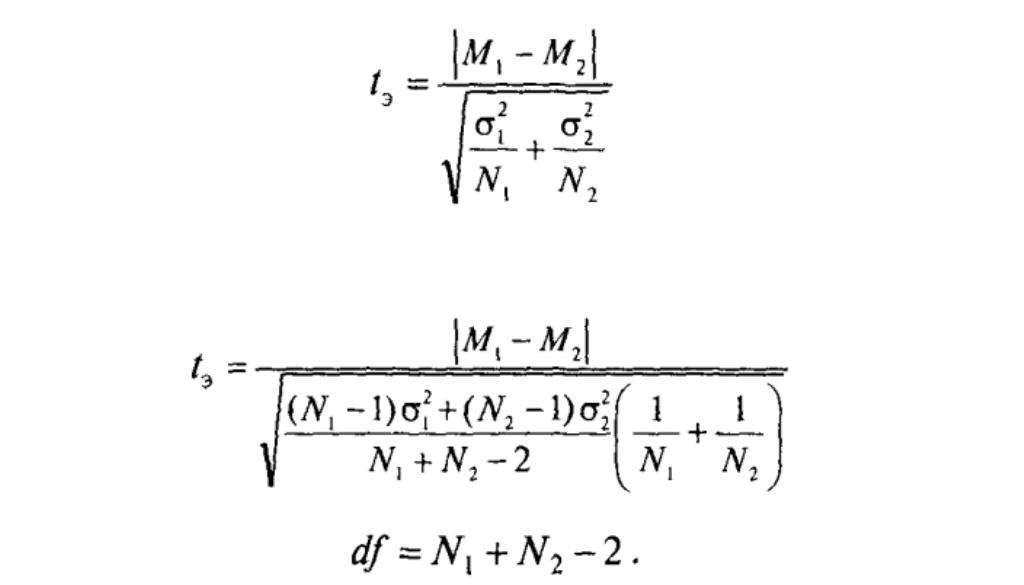
Формула 1 может применяться для приблизительных расчетов, для близких по количеству выборок, а формула 2 — для четких расчетов, когда выборки заметно отличаются по количеству.
Критерии t-Стьюдента для зависимых выборок
Парные t-тесты обычно состоят из совпадающих пар одинаковых единиц или одной группы единиц, которая была дважды проверена («повторное измерение» t-критерия). Когда мы имеем зависимые выборки или два ряда данных, положительно коррелирующих друг с другом, можем, соответственно, оформить статистические гипотезы H0 и H1 и проверить их с помощью данной нам формулы эмпирического значения критерия t-Стьюдента.
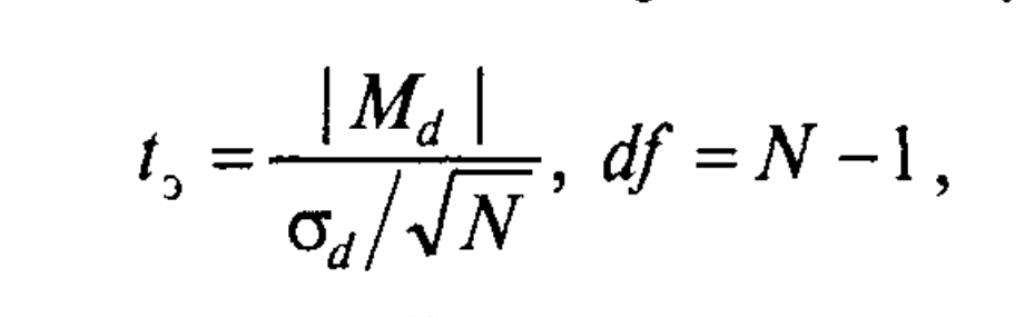
Например, испытуемые подвергаются тестированию до лечения при высоком кровяном давлении и снова тестируются после лечения препаратом для его снижения. Сравнивая те же самые показатели пациентов до и после лечения, мы эффективно используем каждого из них в качестве своего собственного контроля.
Таким образом, правильное отклонение нулевой гипотезы может стать гораздо более вероятным, при этом статистическая сила увеличивается просто потому, что случайная вариация между пациентами теперь устранена. Обратите внимание, однако, что увеличение статистической мощности происходит по оценке: требуется больше тестов, каждый испытуемый должен быть дважды проверен.
Вывод

Форма тестирования гипотез, коэффициент Стьюдента - это лишь один из многих вариантов, используемых для этой цели. Статистики должны дополнительно использовать методы, отличные от t-теста, для изучения большего количества переменных с большими размерами выборки.