Конус - это одна из пространственных фигур вращения, характеристики и свойства которых изучает стереометрия. В данной статье дадим определение этой фигуре и рассмотрим основные формулы, связывающие линейные параметры конуса с его площадью поверхности и объемом.
Что это - конус?
С точки зрения геометрии речь идет о пространственной фигуре, которая образована совокупностью прямых отрезков, соединяющих некоторую точку пространства со всеми точками плавной плоской кривой. Этой кривой может быть окружность или эллипс. На рисунке ниже показан конус.
 Вам будет интересно:Что такое гексоген: состав вещества, получение, применение, мощность
Вам будет интересно:Что такое гексоген: состав вещества, получение, применение, мощность

Представленная фигура не обладает объемом, поскольку стенки ее поверхности имеют бесконечно малую толщину. Однако если ее заполнить веществом и ограничить сверху не кривой, а плоской фигурой, например кругом, то мы получим твердое объемное тело, которое также принято называть конусом.
Форму конуса можно часто встретить в жизни. Так, ею обладает мороженое-рожок или полосатые черно-оранжевые дорожные конусы, которые выставляют на проезжую часть для привлечения внимания участников движения.
Элементы конуса и его виды
Поскольку конус полиэдром не является, то количество образующих его элементов не так велико, как для многогранников. В геометрии конус общего вида состоит из следующих элементов:
- основания, ограничивающая кривая которого называется директрисой, или образующей;
- боковой поверхности, которая является совокупностью всех точек прямых отрезков (генератрис), соединяющих вершину и точки направляющей кривой;
- вершины, являющейся точкой пересечения генератрис.
Заметим, что вершина в плоскости основания не должна лежать, поскольку в этом случае конус вырождается в плоскую фигуру.
Если из вершины провести перпендикулярный отрезок к основанию, то мы получим высоту фигуры. Если последняя основание пересекает в геометрическом центре, то это конус прямой. Если же перпендикуляр не совпадает с геометрическим центром основания, то фигура будет наклонной.
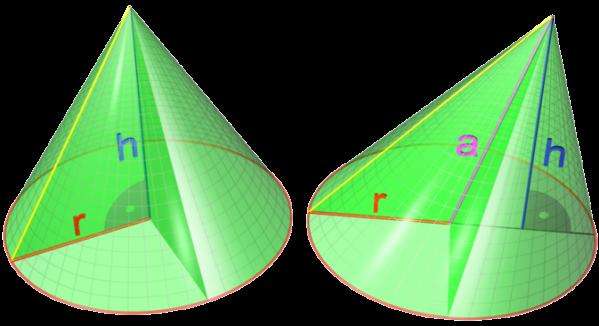
Прямой и наклонный конусы показаны на рисунке. Здесь высота и радиус основания конуса обозначены h и r соответственно. Линия, которая соединяет вершину фигуры и геометрический центр основания, является осью конуса. Из рисунка видно, что для прямой фигуры высота на этой оси лежит, а для наклонной фигуры высота с осью образует некоторый угол. Ось конуса обозначена буквой a.
Прямой конус с круглым основанием
Пожалуй, это конус самый распространенный из рассматриваемого класса фигур. Состоит он из круга и боковой поверхности. Получить геометрическими методами его не представляет никакого труда. Для этого следует взять прямоугольный треугольник и вращать его вокруг оси, совпадающей с одним из катетов. Очевидно, что этот катет станет высотой фигуры, а длина второго катета треугольника образует радиус основания конуса. Схема ниже демонстрирует описанную схему получения рассматриваемой фигуры вращения.
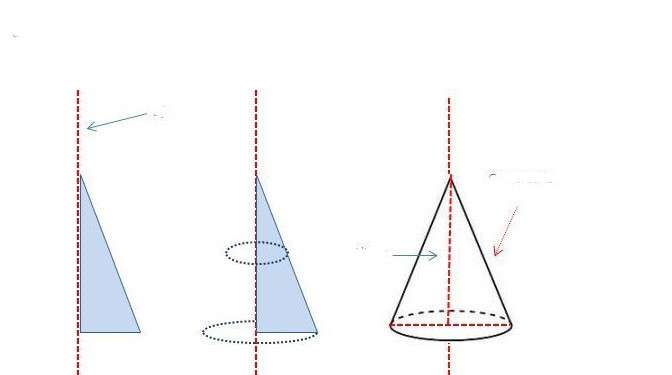
Изображенный треугольник можно вращать вокруг другого катета, при этом получится конус с большим радиусом основания и меньшей высотой, чем первый.
Для однозначного определения всех параметров круглого прямого конуса следует знать любые две его линейных характеристики. Среди них выделяют радиус r, высоту h или длину генератрисы g. Все названные величины являются длинами сторон рассмотренного прямоугольного треугольника, поэтому для их связи справедлива теорема Пифагора:
g2 = r2 + h2.
Площадь поверхности
При изучении поверхности любой объемной фигуры удобно пользоваться ее разверткой на плоскость. Конус не является исключением. Для круглого конуса развертка показана ниже.
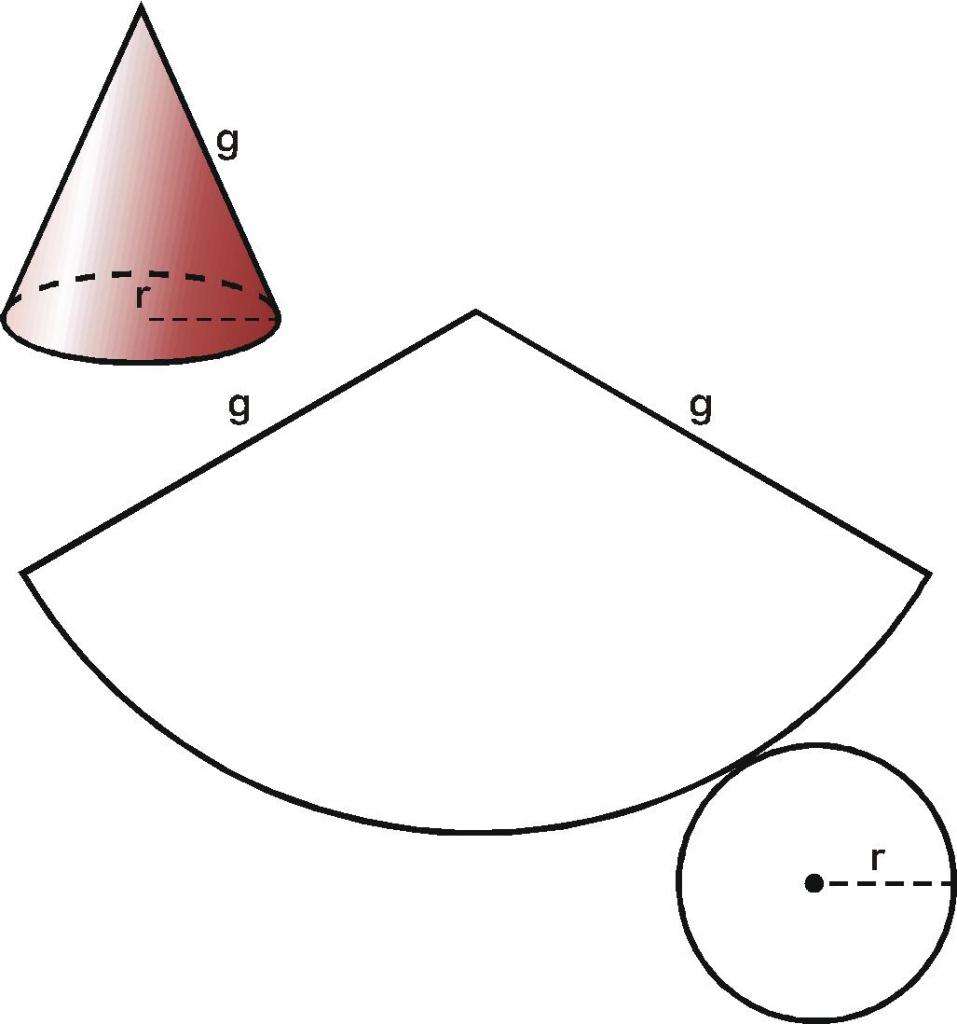
Мы видим, что развертка фигуры состоит из двух частей:
Площадь круга найти легко, и соответствующая формула известна каждому школьнику. Говоря о круговом секторе, заметим, что он является частью круга с радиусом g (длина генератрисы конуса). Длина дуги этого сектора равна длине окружности основания. Эти параметры позволяют однозначно определить его площадь. Соответствующая формула имеет вид:
S = pi*r2 + pi*r*g.
Первое и второе слагаемые в выражении - это конуса основания и боковой поверхности площади соответственно.
Если длина генератрисы g неизвестна, но дана высота h фигуры, тогда формулу можно переписать в виде:
S = pi*r2 + pi*r*√(r2 + h2).
Объем фигуры
Если взять прямую пирамиду и увеличивать на бесконечности число сторон ее основания, то форма основания будет стремиться к окружности, а боковая поверхность пирамиды будет приближаться к конической поверхности. Эти рассуждения позволяют использовать формулу для объема пирамиды при расчете аналогичной величины для конуса. Объем конуса может быть найден по формуле:
V = 1/3*h*So.
Справедлива эта формула всегда, независимо от того, что собой представляет основание конуса, имеющее площадь So. Более того, формула применима также для наклонного конуса.
Поскольку мы изучаем свойства прямой фигуры с круглым основанием, то для определения его объема можно пользоваться таким выражением:
V = 1/3*h*pi*r2.
Справедливость формулы очевидна.
Задача на нахождение площади поверхности и объема
Пусть дан конус, радиус которого равен 10 см, а длина образующей составляет 20 см. Необходимо определить объем и площадь поверхности для этой фигуры.
Для вычисления площади S можно сразу воспользоваться формулой, записанной выше. Имеем:
S = pi*r2 + pi*r*g = 942 см2.
Для определения объема необходимо знать высоту h фигуры. Рассчитаем ее, пользуясь связью между линейными параметрами конуса. Получаем:
h = √(g2 - r2) = √(202 - 102) ≈ 17,32 см.
Теперь можно воспользоваться формулой для V:
V = 1/3*h*pi*r2 = 1/3*17,32*3,14*102 ≈ 1812,83 см3.
Отметим, что объем круглого конуса составляет третью часть от цилиндра, в который он вписан.

