Все пространственные фигуры, которые изучает специальный раздел геометрии - стереометрия, можно согласно их форме разделить на два типа: многогранники (полиэдры) и фигуры, образованные гладкими поверхностями. Об одной из фигур второго типа пойдет речь в статье. Мы популярно ответим на вопрос "что такое конус".
Определение фигуры
Предположим, что имеется некоторая плоская замкнутая кривая, например окружность или эллипс. В пространстве выберем некоторую точку, которая не принадлежит плоскости указанной кривой. Теперь соединим ее с каждой точкой на кривой при помощи прямых отрезков. Полученная фигура дает ответ на вопрос о том, что такое конус. На фото ниже показаны три конуса, изготовленные из бумаги.
Вам будет интересно:Главные города Древнего Рима: названия, история
Исходная замкнутая кривая называется директрисой или направляющей фигуры. Фиксированная точка в пространстве, упомянутая выше, называется вершиной конуса. Прямые отрезки, которые соединяют вершину с точками на директрисе, получили название генератрис, или образующих.
Вам будет интересно:Виды, сущность и понятие национальной безопасности РФ
Рассматриваемая фигура образует некоторую поверхность, поэтому объемом не обладает. Если же внутри эту фигуру заполнить каким-либо веществом, то у нее появится некоторый объем. Полученное твердое тело также называется конусом.
Элементы конуса
Под элементами фигуры понимают геометрические объекты, из которых она состоит. Зная, что такое конус, можно сказать, что основными его элементами являются следующие:
- Основание - плоская фигура, ограниченная директрисой. Например, это может быть круг.
- Боковая поверхность. Она также называется конической и образована совокупностью точек всех генератрис.
- Вершина - точка, не принадлежащая основанию, в которой пересекаются все генератрисы.
Конус от полиэдров (многогранников) отличает то, что он не имеет граней и ребер, поскольку образован гладкой боковой конической поверхностью. С точки зрения математики, конус - это пирамида с бесконечным числом сторон.
Виды конуса
Мы узнали, что такое конус. Теперь перейдем к рассмотрению вопроса о том, какие виды фигур бывают.
В зависимости от кривой, находящейся в основании, говорят о конусе круглом, эллиптическом, гиперболическом, параболическом и так далее. Кроме того, фигура может быть прямой и наклонной. Чтобы понять разницу между ними, следует познакомиться с понятием высоты.
Высота конуса - это длина отрезка, который перпендикулярно из вершины фигуры опущен к плоскости ее основания. Если высота пересекает основание в геометрическом центре (центр круга или эллипса), то конус называется прямым. В противном случае говорят о фигуре наклонной. Рисунок ниже демонстрирует два конуса. Левый является прямым, правый - наклонным.
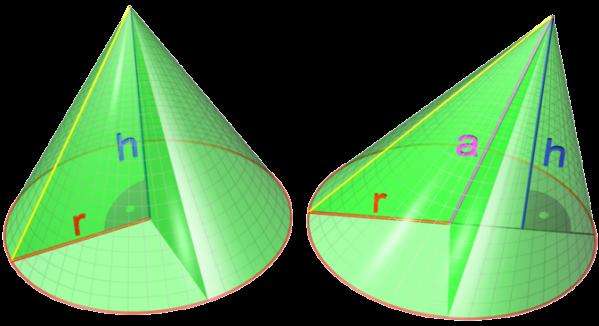
В большинстве геометрических задач рассматривают прямой конус с круглым основанием. Далее в статье дадим подробную характеристику этой фигуре.
Как можно получить круглый прямой конус?
Выше было дано определение конуса и один из способов его геометрического построения. Поскольку круглый прямой конус - это тело вращения, то его получить можно следующим простым способом: возьмем произвольный треугольник с прямым углом. Предположим, что два катета этого треугольника будут равны a и b. Поставим треугольник на один из катетов, например a. И будем его вращать вокруг второго катета b. Гипотенуза треугольника при этом опишет коническую поверхность.
В результате описанного способа получения круглого конуса образуется фигура, имеющая радиус основания a и высоту b. Катет b является частью оси конуса, которая проходит через его вершину и центр основания. Гипотенуза исходного треугольника будет генератрисой фигуры.
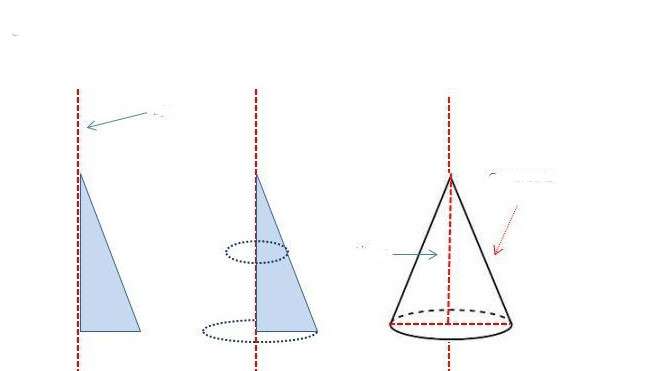
Схема выше показывает, как можно получить конус, вращая прямоугольный треугольник вокруг одного из катетов.
Линейные характеристики круглого прямого конуса
Фигура образована кругом некоторого радиуса r и конической поверхностью. Пусть высота конуса равна h. Указанные две линейные характеристики являются основными. Их знание позволяет вычислить любые параметры фигуры, например, длину его генератрис, площадь поверхности и объем.
Поскольку рассматриваемая фигура является прямой, то длины всех его генератрис равны между собой. Если обозначить их длину буквой d, тогда формула для ее вычисления будет иметь вид:
d = √(h2 + r2).
Нетрудно догадаться, откуда взялась эта формула. Она является результатом применения теоремы Пифагора к соответствующему прямоугольному треугольнику. Отметим, что генератриса конуса всегда больше радиуса его основания, независимо от значения величины h.
Данное выражение позволяет по двум известным линейным величинам определить третью. Например, если известны d и h, тогда радиус круга в основании будет равен:
r = √(d2 - h2).
Поверхность и объем
Как было отмечено, площадь поверхности фигуры равна сумме площадей ее основания и боковой поверхности. Формула для площади основания совпадает с таковой для круга. Что касается боковой поверхности, если представить ее в виде развертки, то можно увидеть, что представляет она сектор круга радиусом d. Здесь d - длина генератрисы. Развертка конуса показана ниже.
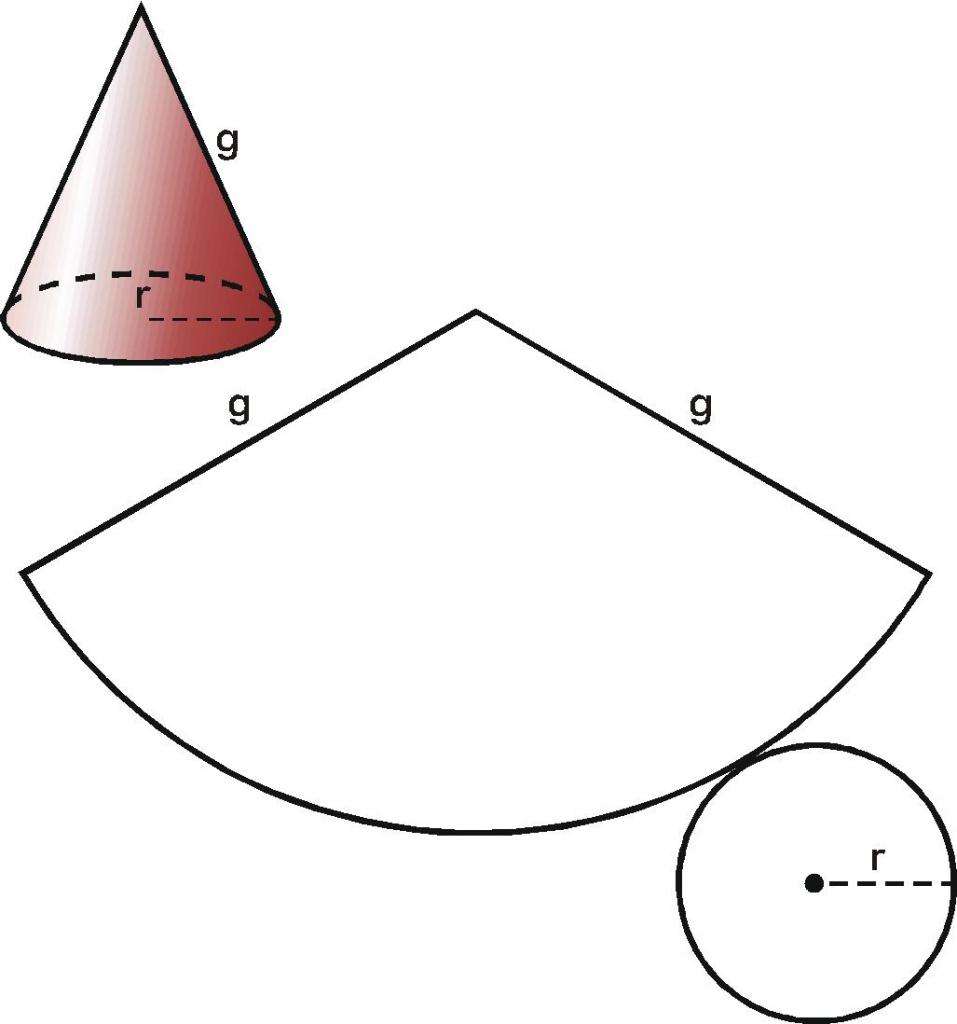
Пусть высота конуса равна h, а его радиус основания - r, тогда для площади поверхности рассматриваемой фигуры справедливо следующее равенство:
S = pi*r2 + pi*r*√(r2 + h2).
Здесь первое слагаемое отражает площадь основания, второе слагаемое - площадь конической поверхности. Можно заметить, что подкоренное выражение соответствует длине генератрисы d. Формула для площади конической поверхности получается, если рассмотреть параметры круглого сектора, показанного на развертке выше. Заметим, что длина дуги этого сектора равна директрисе основания фигуры.
Объем конуса произвольного типа рассчитывается по следующей формуле:
V = 1/3*h*So.
Здесь символом So обозначена площадь основания. Заметим, что аналогичная формула и у объема пирамиды. Это совпадение не является случайным, поскольку увеличение числа граней пирамиды до бесконечности переводит ее в конус.
Записанная формула для случая прямого круглого конуса приобретает конкретный вид:
V = pi/3*h*r2 .
Здесь множитель pi*r2 является площадью основания (круга).
Таким образом, объем прямого конуса, основанием которого является круг, равен одной трети объема цилиндра, имеющего тот же радиус и ту же высоту.