При изучении свойств фигур в трехмерном пространстве в рамках стереометрии часто приходится решать задачи на определение объема и площади поверхности. В данной статье покажем, как для усеченной пирамиды объем и площадь боковой поверхности вычислить, используя известные формулы.
Пирамида в геометрии
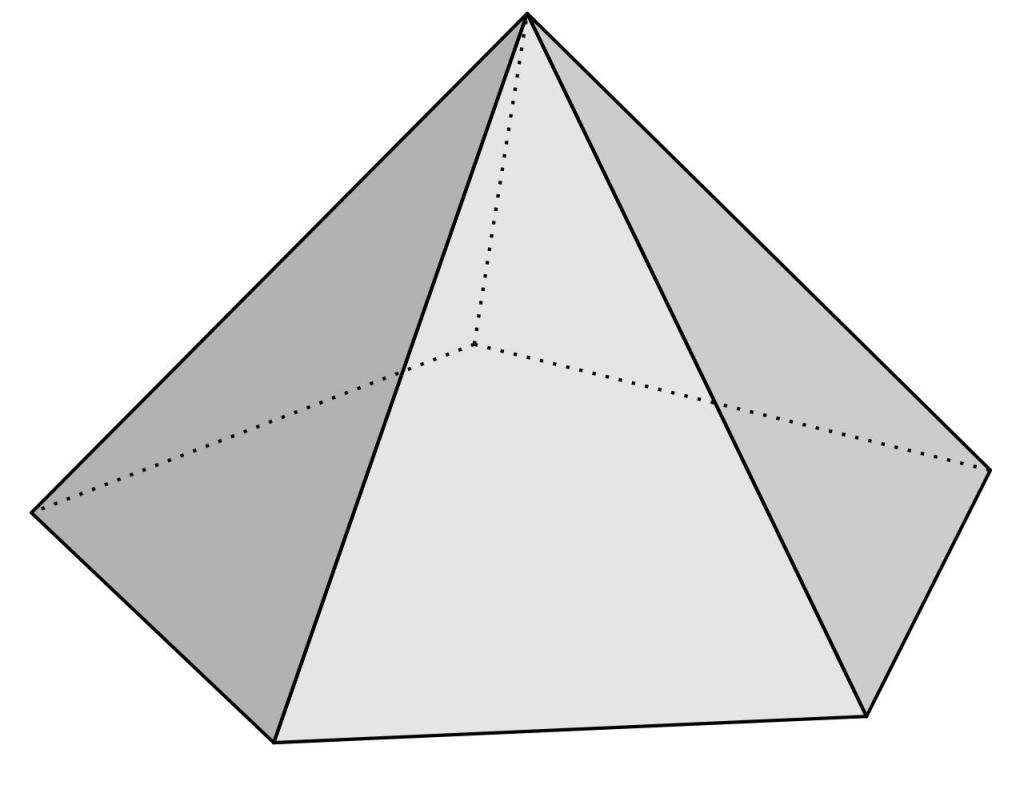
В геометрии обычной пирамидой называют фигуру в пространстве, которая построена на некотором плоском n-угольнике. Все вершины его соединены с одной точкой, расположенной вне плоскости многоугольника. Для примера приведем фото, где изображена пятиугольная пирамида.
 Вам будет интересно:Вывод формулы площади конуса. Пример решения задачи
Вам будет интересно:Вывод формулы площади конуса. Пример решения задачи
Эта фигура образована гранями, вершинами и ребрами. Пятиугольная грань называется основанием. Остальные треугольные грани образуют боковую поверхность. Точка пересечения всех треугольников - это главная вершина пирамиды. Если из нее опустить перпендикуляр на основание, то возможны два варианта положения точки пересечения:
- в геометрическом центре, тогда пирамида называется прямой;
- не в геометрическом центре, тогда фигура будет наклонной.
Далее будем рассматривать только прямые фигуры с правильным n-угольным основанием.
Что это за фигура - усеченная пирамида?
Чтобы определить объем усеченной пирамиды, необходимо четко понимать, о какой фигуре конкретно идет речь. Внесем ясность в этот вопрос.
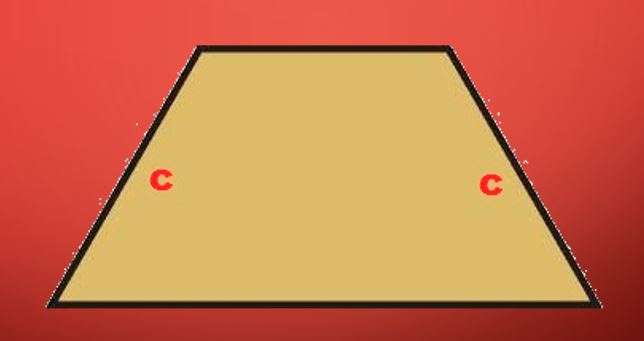
Предположим, что мы взяли секущую плоскость, которая параллельна основанию обычной пирамиды, и отсекли с помощью нее часть боковой поверхности. Если эту операцию проделать с изображенной выше пятиугольной пирамидой, то получится такая фигура, как на рисунке ниже.

Из фото видно, что эта пирамида имеет уже два основания, причем верхнее является подобным нижнему, но по размерам оно меньше. Боковая поверхность представлена уже не треугольниками, а трапециями. Они являются равнобедренными, а их число соответствует количеству сторон основания. Усеченная фигура не имеет главной вершины, как обычная пирамида, а ее высота определяется расстоянием между параллельными основаниями.
В общем случае, если рассматриваемая фигура образована n-угольными основаниями, она имеет n+2 грани, или стороны, 2*n вершин и 3*n ребер. То есть усеченная пирамида является многогранником.
Формула объема усеченной пирамиды
Напомним, что объем обычной пирамиды равен 1/3 произведения ее высоты и площади основания. Для усеченной пирамиды эта формула не подходит, поскольку она имеет два основания. А ее объем будет всегда меньше, чем аналогичная величина для обычной фигуры, из которой она получена.
Не вдаваясь в математические подробности получения выражения, приведем конечную формулу для объема усеченной пирамиды . Она записывается в следующем виде:
V = 1/3*h*(S1 + S2 + √(S1*S2))
Здесь S1 и S2 - площади нижнего и верхнего оснований соответственно, h - высота фигуры. Записанное выражение является справедливым не только для прямой правильной усеченной пирамиды, но и для любой фигуры данного класса. Причем независимо от вида многоугольников основания. Единственным условием, ограничивающим применение выражения для V, является необходимость параллельности друг другу оснований пирамиды.
Несколько важных выводов можно сделать, изучая свойства этой формулы. Так, если площадь верхнего основания равна нулю, тогда мы приходим к формуле для V обычной пирамиды. Если же площади оснований равны друг другу, то получаем формулу для объема призмы.
Как определить площадь боковой поверхности?
Знание характеристик усеченной пирамиды предполагает не только умение рассчитывать ее объем, но и знать, как определять площадь боковой поверхности.
Пирамида усеченная состоит из двух типов граней:
- равнобедренные трапеции;
- многоугольные основания.
Если в основаниях находится правильный многоугольник, то расчет его площади не представляет больших трудностей. Для этого нужно знать лишь длину стороны a и их количество n.
В случае с боковой поверхностью расчет ее площади предполагает определение этой величины для каждой из n трапеций. Если n-угольник является правильным, то формула для площади боковой поверхности принимает вид:
Sb = hb*n*(a1+a2)/2
Здесь hb - высота трапеции, которая называется апотемой фигуры. Величины a1 и a2 - это длины сторон правильных n-угольных оснований.
Для каждой правильной n-угольной усеченной пирамиды можно однозначно определить апотему hb через параметры a1 и a2 и высоту h фигуры.
Задача на вычисление объема и площади фигуры
Дана правильная треугольная усеченная пирамида. Известно, что ее высота h равна 10 см, а длины сторон оснований равны 5 см и 3 см. Чему равны объем усеченной пирамиды и площадь ее боковой поверхности?
Сначала вычислим величину V. Для этого следует найти площади равносторонних треугольников, находящихся в основаниях фигуры. Имеем:
S1 = √3/4*a12 = √3/4*52 = 10,825 см2;
S2 = √3/4*a22 = √3/4*32 = 3,897 см2
Подставляем данные в формулу для V, получаем искомый объем:
V = 1/3*10*(10,825 + 3,897 + √(10,825 *3,897 )) ≈ 70,72 см3
Чтобы определить боковую поверхность, следует знать длину апотемы hb. Рассматривая соответствующий прямоугольный треугольник внутри пирамиды, можно для него записать равенство:
hb = √((√3/6*(a1 - a2))2 + h2) ≈ 10,017 см
Значение апотемы и сторон треугольных оснований подставляем в выражение для Sb и получаем ответ:
Sb = hb*n*(a1+a2)/2 = 10,017*3*(5+3)/2 ≈ 120,2 см2
Таким образом, мы ответили на все вопросы задачи: V ≈ 70,72 см3, Sb ≈ 120,2 см2.