Каждый школьник слышал о фигуре конус. Его свойства и характеристики изучает стереометрия. Из этой фигуры можно получить ее усеченный вариант. В данной статье рассмотрим вопрос, что такое развертка усеченного конуса и как найти ее площадь.
Какую фигуру будем изучать?
Круглый прямой усеченный конус представляет собой два круга, имеющих разный диаметр, которые расположены в параллельных плоскостях. Окружности этих кругов соединены прямыми отрезками равной длины, именуемых образующими фигуры. Расстояние между круглыми основаниями называется высотой. Описанная фигура показана ниже на фото.
Вам будет интересно:Технология исследовательской деятельности: понятие, внедрение нового, разработка проектов, цели и задачи
Получить ее можно двумя принципиально отличающимися геометрическими способами. Во-первых, можно взять обычный круглый конус и параллельной его основанию плоскостью отсечь верхнюю часть. Такое действие приведет к образованию верхнего (малого) основания усеченного конуса. Во-вторых, можно взять трапецию с двумя прямыми углами и вращать ее вокруг стороны, ограниченной этими углами. Сторона трапеции, вокруг которой будет происходить вращение, называется осью фигуры. Две параллельные стороны трапеции опишут круглые основания во время вращения, а четвертая наклонная сторона образует боковую поверхность фигуры.
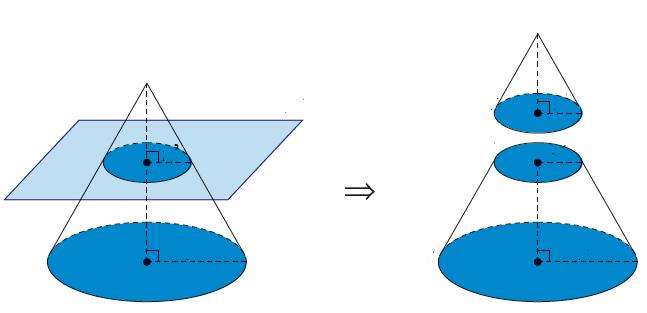
Схема выше демонстрирует получение усеченного конуса с помощью сечения плоскостью.
Развертка усеченного конуса
Как мы видели, рассматриваемая фигура образована тремя поверхностями. Две из них представляют основания, а третья является боковой. Сумма площадей этих поверхностей является полной поверхностью усеченного конуса. В трехмерном пространстве ее площадь вычислять неудобно, поскольку сама величина является двумерной. В связи с этим при возникновении проблемы определения площади поверхности пространственных фигур, их принято представлять на плоскости.
В нашем случае развертку получить достаточно просто. Для этого следует мысленно отрезать по соответствующим окружностям основания от фигуры. Затем, необходимо разрезать вдоль образующей и раскрыть поверхность боковую. В итоге получится результат, показанный на фото.
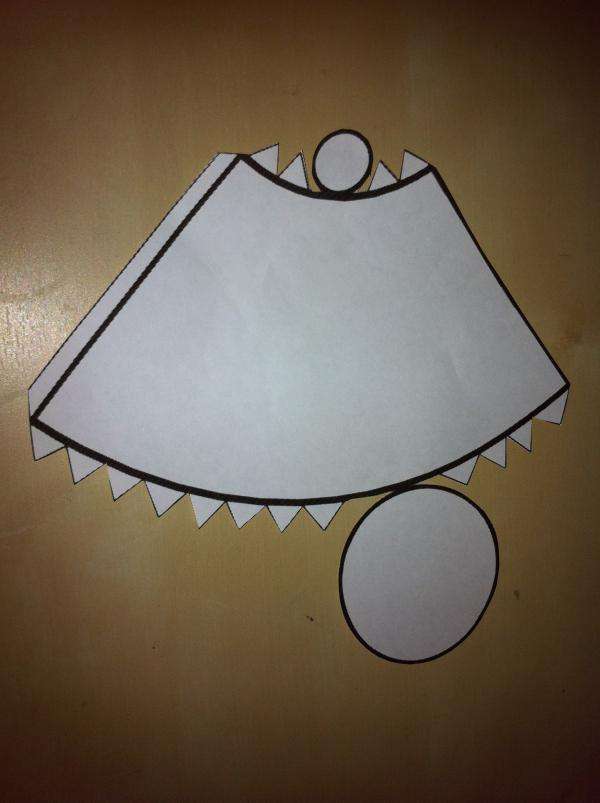
Она представляет собой два разных круга и часть кругового сектора, у которого вырезан центр.
Формула площади поверхности фигуры
Для вычисления площади поверхности усеченного конуса необходимо определить эту величину для каждой части его развертки. Обозначим радиусы оснований буквами R и r. Тогда их площади будут равны:
So1 = pi*R2;
So2 = pi*r2.
Для вычисления площади боковой поверхности учтем, что ее развертка образована двумя одинаковыми генератрисами g и двумя дугами окружностей, которые имеют длину 2*pi*r и 2*pi*R. Опуская рассуждения и промежуточные математические формулы, приведем конечное выражение для площади этой части развертки фигуры. Оно имеет форму:
Sb = pi*g*(R + r).
Получив площади для оснований и боковой поверхности, можно записать формулу развертки конуса усеченного. Ее общая площадь S равна:
S = So1 + So2 + Sb = pi*(R2 + r2 + g*(R + r)).
Таким образом, площадь S фигуры однозначно определяется из знания радиусов ее оснований и длины генератрисы.
Геометрическая задача
Необходимо провести расчет развертки усеченного конуса, который имеет высоту 13 см и радиусы оснований 2 см и 7 см.
Решение данной задачи с помощью непосредственного применения формулы для S невозможно, поскольку не известна длина генератрисы g. Тем не менее, ее можно вычислить, используя такую формулу:
g = √(h2 + (R-r)2).
Это выражение можно самостоятельно получить, рассмотрев прямоугольный треугольник со сторонами g, h и (R-r), здесь h - высота усеченного конуса. Генератриса g будет равна 13,93 см (значение приведено с точностью до 0,01 см).
Осталось подставить значения генератрисы и радиусов в формулу для S, чтобы получить требуемый ответ:
S = 3,14*(72 + 22 + 13,93*(7 + 2)) ≈ 560,1 см2.
Следует не забывать, что записанная для S формула справедлива только для круглого прямого усеченного конуса.
