В школьном курсе стереометрии изучают свойства разных пространственных фигур. Одной из них является пирамида. Данная статья посвящена вопросу о том, как найти у пирамиды площадь боковой поверхности. Также раскрывается вопрос определения этой площади для усеченной пирамиды.
Что такое пирамида?
Многие, услышав слово "пирамида", сразу представляют грандиозные сооружения Древнего Египта. Действительно, гробницы Хеопса и Хефрена являются правильными четырехугольными пирамидами. Тем не менее пирамидой также является тетраэдр, фигуры с пяти-, шести-, n-угольным основанием.
Вам будет интересно:Советская космическая программа. Космические корабли и орбитальные станции
В геометрии понятие пирамиды определено четко. Под этой фигурой понимают объект в пространстве, который образуется в результате соединения некоторой точки с углами плоского n-угольника, где n - целое число. Ниже рисунок показывает четыре пирамиды с разным количеством углов в основании.
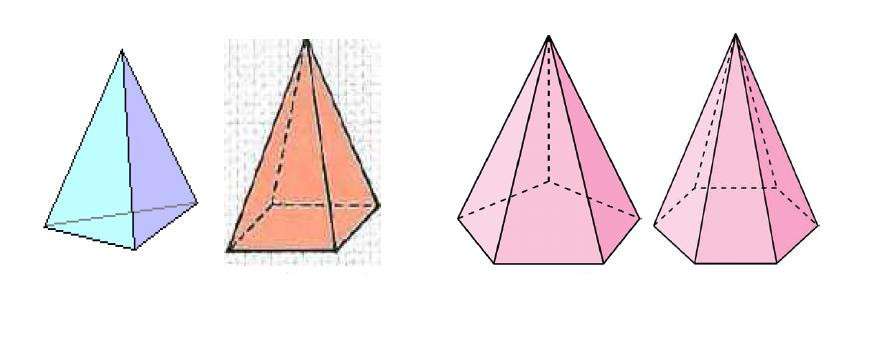
Точка, с которой соединены все вершины углов основания, не лежит в его плоскости. Она называется вершиной пирамиды. Если из нее провести к основанию перпендикуляр, то мы получим высоту. Фигура, в которой высота пересекает основание в геометрическом центре, получила название прямой. Иногда прямая пирамида имеет правильное основание, например квадрат, равносторонний треугольник и так далее. В этом случае она называется правильной.
При вычислении у пирамиды площади боковой поверхности удобно работать с правильными фигурами.
Площадь поверхности боковой фигуры
Как найти у пирамиды площадь боковой поверхности? Можно понять это, если ввести соответствующее определение и рассмотреть развертку на плоскости для этой фигуры.
Любая пирамида образована гранями, которые друг от друга отделены ребрами. Основание - это грань, образованная n-угольником. Все остальные грани представляют собой треугольники. Их n штук, и они все вместе образуют боковую поверхность фигуры.
Если вдоль бокового ребра разрезать поверхность и развернуть ее на плоскости, то получится развертка пирамиды. Для примера ниже показана развертка шестиугольной пирамиды.
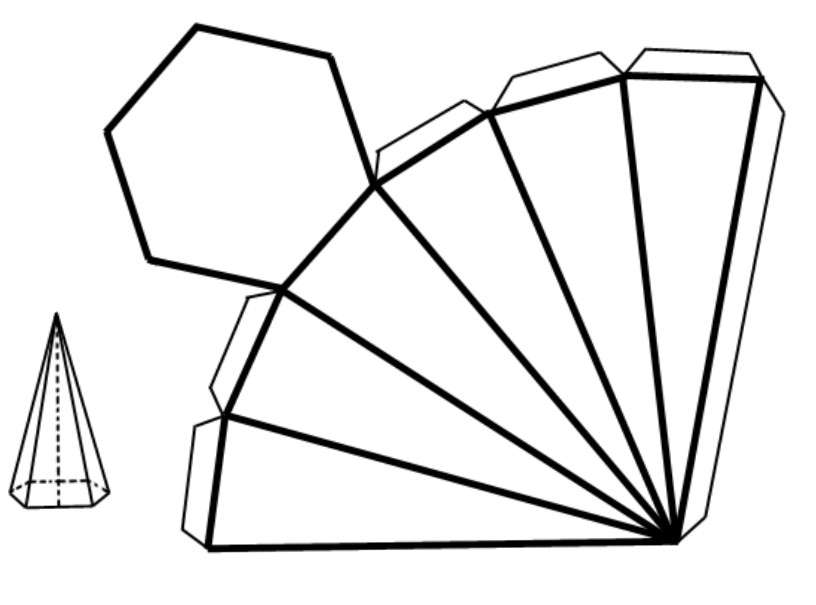
Видно, что боковая поверхность образована шестью одинаковыми треугольниками.
Теперь не трудно догадаться, как у пирамиды найти площадь боковой поверхности. Для этого следует сложить площади всех треугольников. В случае n-угольной правильной пирамиды, сторона основания которой равна a, для рассматриваемой поверхности можно записать формулу:
Sb = n*a*hb/2
Здесь hb - это апофема пирамиды. То есть высота треугольника, опущенная из вершины фигуры на сторону основания. Если апофема неизвестна, то ее можно рассчитать, зная параметры n-угольника и значение высоты h фигуры.
Усеченная пирамида и ее поверхность
Как можно догадаться из названия, усеченную пирамиду можно получить из обычной фигуры. Для этого нужно отсечь плоскостью, параллельной основанию, вершину. Ниже рисунок демонстрирует этот процесс для шестиугольной фигуры.
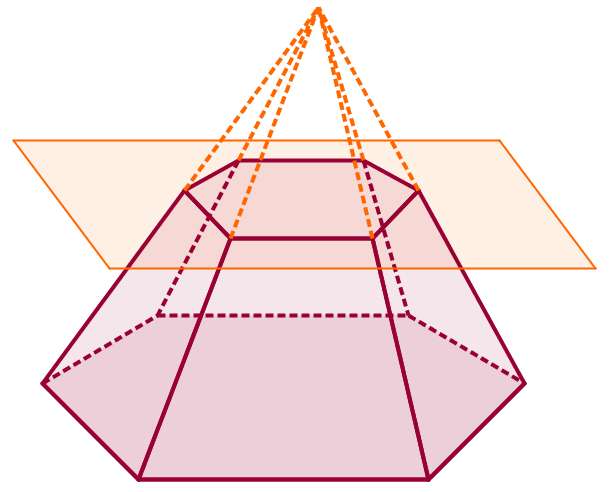
Ее боковая поверхность представляет собой сумму площадей одинаковых равнобедренных трапеций. Формула для площади боковой поверхности усеченной пирамиды (правильной) имеет вид:
Sb = hb*n*(a1 + a2)/2
Здесь hb - апофема фигуры, которая является высотой трапеции. Величины a1 и a2 - это длины оснований сторон.
Расчет боковой поверхности для треугольной пирамиды
Покажем, как найти площадь боковой поверхности пирамиды. Допустим, у нас правильная треугольная, разберемся на примере конкретной задачи. Известно, что сторона основания, представляющего собой равносторонний треугольник, равна 10 см. Высота фигуры равна 15 см.
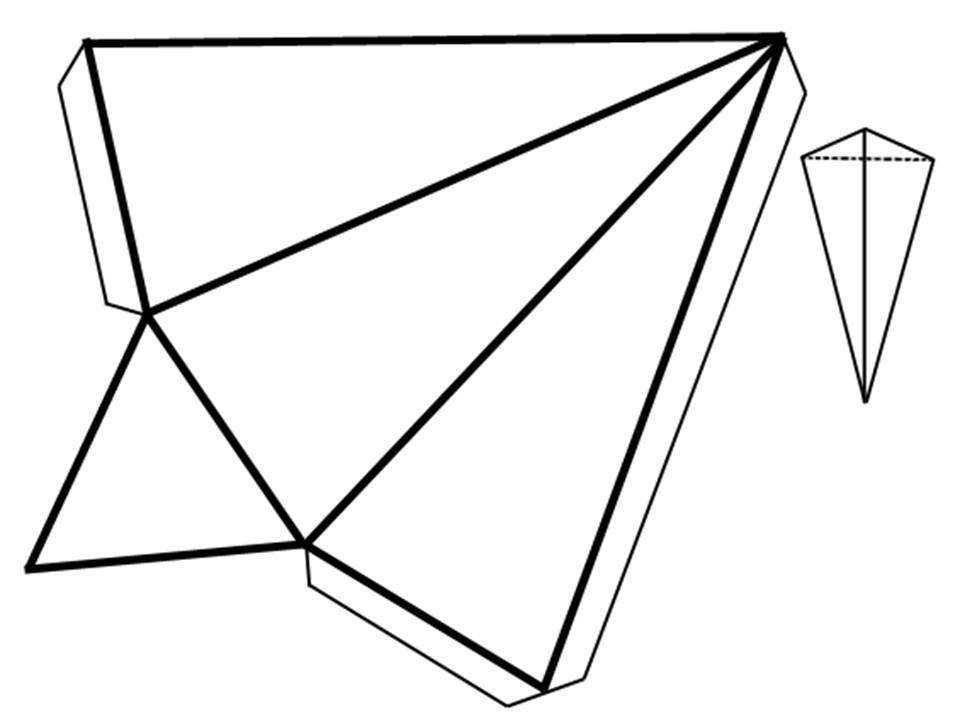
Развертка этой пирамиды показана на рисунке. Чтобы воспользоваться формулой для Sb, необходимо сначала найти апофему hb. Рассматривая прямоугольный треугольник внутри пирамиды, построенный на сторонах hb и h, равенство можно записать следующее:
hb = √(h2+a2/12)
Подставляем данные и получаем, что hb≈15,275 см.
Теперь можно воспользоваться формулой для Sb:
Sb = n*a*hb/2 = 3*10*15,275/2 = 229,125 см2
Заметим, что основание треугольной пирамиды, как и ее боковая грань, образовано треугольником. Тем не менее этот треугольник при вычислении площади Sb не учитывается.