Каждый школьник знает, что такое окружность и какими параметрами она характеризуется. Движение по круговой траектории является одним из распространенных в природе видов перемещения объектов. Что это - равномерное движение по окружности, и какими формулами оно описывается, расскажем в данной статье.
Движение вращения
Чтобы яснее понять, о чем идет речь, сразу приведем примеры этого вида перемещения тел в пространстве. Примерами являются:
- вращение металлического вала;
- движение колеса автомобиля или велосипеда;
- раскручивание камня, привязанного к веревке;
- вращения игрушки-юлы;
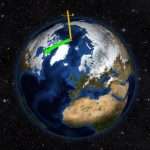
- движение нашей планеты вокруг Солнца и вокруг собственной оси.
Вам будет интересно:Генерал Андреев Андрей Матвеевич: биография, военная служба, награды, память
Элементами, которые характеризуют рассматриваемый вид движения, являются:
- Окружность, которая обладает некоторым радиусом r. Окружность является траекторией движения.
- Ось, вокруг которой происходит вращение. Она расположена в центре окружности в перпендикулярной ей плоскости.
Вам будет интересно:Вращательное движение твердого тела: уравнение, формулы
В физике для описания любого перемещения объектов применяют набор кинематических величин. Далее приведем эти величины для вращательного движения.
Угловые характеристики вращения
К ним относятся угол поворота θ, угловая скорость ω и угловое ускорение α. В физике равномерного движения по окружности эти три величины принимают определенное значение.
Что касается угла θ, то его физический смысл интуитивно понятен. Величина θ показывает центральный угол кругового сектора, на который тело поворачивается за известный промежуток времени. Далее в формулах его выражают в радианах. Напомним, что полная окружность соответствует 2*pi радианам.
Скорость ω является аналогом линейной величины, только ее единицами измерения являются радианы в секунду. В дифференциальной форме математическое определение величины ω выглядит так:
ω = dθ/dt
Угловая скорость показывает быстроту вращения тела. Ее можно использовать для расчета частоты вращения f в оборотах в секунду. Для этого используют формулу:
f = ω/(2*pi)
Ускорение α показывает, как быстро изменяется скорость вращения ω. То есть для него справедливо выражение:
α = dω/dt
Единицей измерения для величины α являются радианы в квадратную секунду (рад/с2).
Что это - равномерное движение по окружности?
В физике 10 класса подробно изучают рассматриваемую тему. Каждый знает, что прямолинейное движение будет равномерным, если линейная скорость v тела остается постоянной. В случае же вращательного движения можно дать следующее определение: равномерное движение по окружности - это вращение тела с постоянной угловой скоростью. Поскольку последняя не меняется, то угловое ускорение α равно нулю. Приведенные рассуждения позволяют записать основную формулу, описывающую рассматриваемый вид перемещения тел:
θ = ω*t
В выражении ω = const, а величины θ и t изменяются. Графическим представлением этого типа движения является прямая линия, которая проходит через начало координат. Тангенс угла между этой линией и осью x равен модулю угловой скорости ω.
Особенность равномерного движения по окружности - это прохождение телом за одинаковые промежутки времени одинаковых угловых отрезков. Эта особенность отличает равномерное вращение от ускоренного.
Линейная и угловая скорость при равномерном движении по окружности
До настоящего времени кинематика вращательного движения рассматривалась в рамках угловых характеристик. Их использование является удобным для решения практических задач. Тем не менее иногда оказывается полезным знать линейные характеристики вращающейся системы. Важной из них является линейная скорость v.
Чтобы найти связь между величинами v и ω, предположим, что вращение материальной точки осуществляется по окружности радиусом r. Тогда линейная скорость при равномерном движении по окружности - это величина, которая рассчитывается по формуле:
v = 2*pi*r/t
Где t - время совершения телом одного оборота вокруг оси вращения. Угловая скорость ω при этом может быть рассчитана так:
ω = 2*pi/t
Сравнивая эти выражения, приходим к формуле:
v = ω*r
Таким образом, линейная скорость для материальной точки, вращающейся по круговой траектории с радиусом r, является величиной постоянной. Однако если рассматривается вращение массивного тела, то линейная скорость каждой его точки будет возрастать с увеличением расстояния до оси вращения, а величина ω при этом остается постоянной.
Центростремительное ускорение
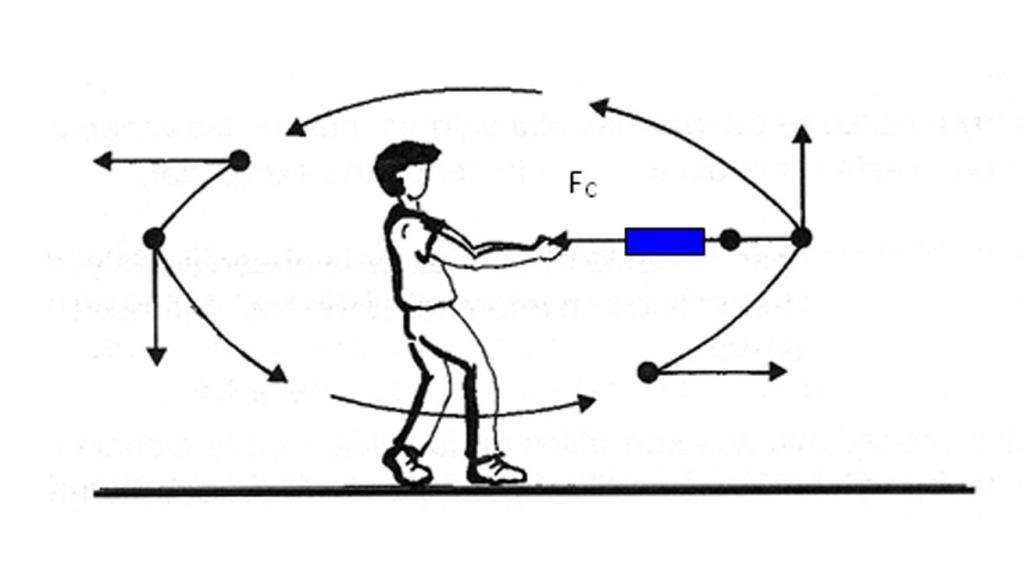
Чтобы тело имело возможность вращаться по окружности, необходимо присутствие некоторой силы, которая по отношению к вращающейся системе является внутренней. Эта сила обеспечивает искривление прямолинейной траектории движения любого тела, обладающего инерционными свойствами. Речь идет о центростремительной силе, которая направлена от центра масс тела к оси вращения. Равномерное движение по окружности и центростремительное движение - это один и тот же процесс. Если бы не было центростремительной силы, то вращение было бы невозможно.
Согласно законам Ньютона, действие на тело любой силы приводит к появлению ускорения. При равномерном движении по окружности не существует углового ускорения (оно равно нулю), однако существует центростремительное ускорение. Его рассчитывают по формуле:
ac = v2/r
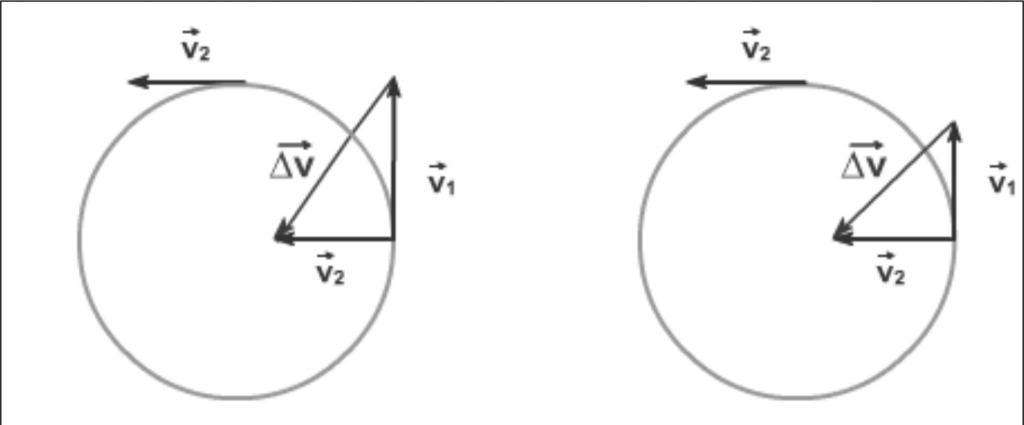
Ускорение ac не приводит к изменению модуля скоростей v и ω. Результатом его действия является изменение направления вектора v.
Решение задачи
Полагая движение нашей планеты вокруг Солнца равномерным, необходимо найти значение центростремительного ускорения, с которым солнечная гравитация действует на Землю.
Через угловую скорость можно записать следующую формулу для ac:
ac = ω2*r
В свою очередь величина ω для Земли определяется по формуле:
ω = 2*pi/T
Тогда получаем для центростремительного ускорения ac:
ac = 4*pi2*r/T2
Где r - среднее расстояние от земли до светила, T - земной год. Учитывая, что r = 149,6 млн км, T = 365,3 дня, получаем ответ: ac = 0,006 м/с2. Эта величина в сотни раз меньше типичных линейных ускорений при движении транспортных средств.