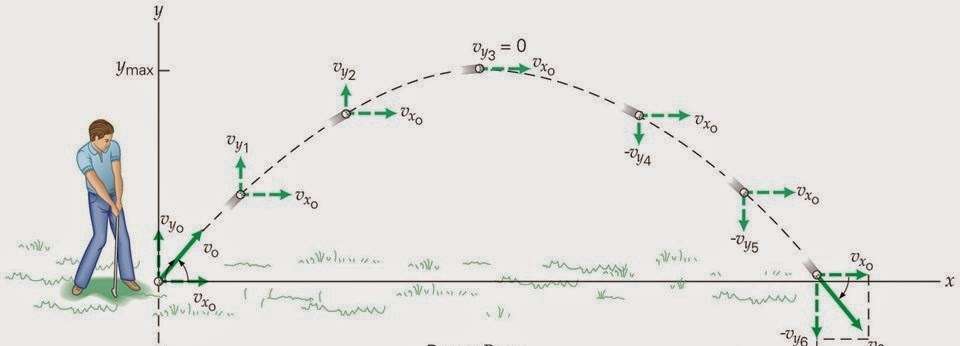
Когда изучают механическое движение в физике, то после ознакомления с равномерным и равноускоренным перемещением объектов, переходят к рассмотрению движения тела под углом к горизонту. В данной статье изучим подробнее этот вопрос.
Что собой представляет движение тела под углом к горизонту?
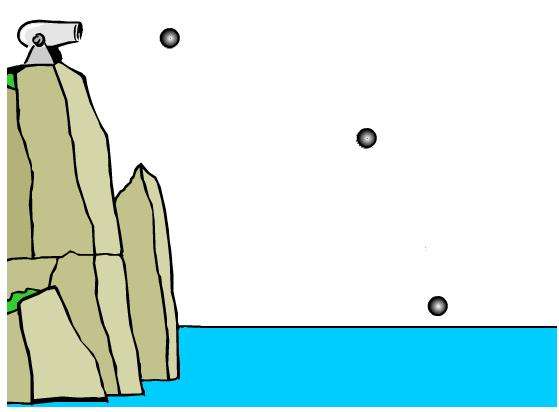
Этот тип перемещения объектов возникает, когда человек бросает камень в воздух, пушка совершает выстрел ядром, или вратарь выбивает от ворот футбольный мяч. Все подобные случаи рассматриваются наукой баллистикой.
 Вам будет интересно:Школьная география: где на карте мира находится Австрия
Вам будет интересно:Школьная география: где на карте мира находится Австрия
Отмеченный вид перемещения объектов в воздухе происходит по параболической траектории. В общем случае проведение соответствующих расчетов является делом не простым, поскольку необходимо учитывать сопротивление воздуха, вращение тела во время полета, вращение Земли вокруг оси и некоторые другие факторы.
В данной статье мы не будем учитывать все эти факторы, а рассмотрим вопрос с чисто теоретической точки зрения. Тем не менее, полученные формулы достаточно хорошо описывают траектории тел, перемещающихся на небольшие расстояния.
Получение формул для рассматриваемого вида движения

Выведем формулы движения тела к горизонту под углом. При этом будем учитывать только одну-единственную силу, действующую на летящий объект - силу тяжести. Поскольку она действует вертикально вниз (параллельно оси y и против нее), то, рассматривая горизонтальную и вертикальную составляющие движения, можно сказать, что первая будет иметь характер равномерного прямолинейного перемещения. А вторая - равнозамедленного (равноускоренного) прямолинейного перемещения с ускорением g. То есть, компоненты скорости через значение v0 (начальная скорость) и θ (угол направления движения тела) запишутся так:
vx = v0*cos(θ)
vy = v0*sin(θ)-g*t
Первая формула (для vx) справедлива всегда. Что касается второй, то тут нужно отметить один нюанс: знак минус перед произведением g*t ставится только в том случае, если вертикальная компонента v0*sin(θ) направлена вверх. В большинстве случаев так и происходит, однако, если бросить тело с высоты, направив его вниз, тогда в выражении для vy следует поставить знак "+" перед g*t.
Проинтегрировав формулы для компонент скорости по времени, и учитывая начальную высоту h полета тела, получаем уравнения для координат:
x = v0*cos(θ)*t
y = h+v0*sin(θ)*t-g*t2/2
Вычисление дальности полета
При рассмотрении в физике движения тела к горизонту под углом, полезным для практического применения, оказывается расчет дальности полета. Определим ее.
Поскольку это перемещение представляет собой равномерное движения без ускорения, то достаточно подставить в него время полета и получить необходимый результат. Дальность полета определяется исключительно перемещением вдоль оси x (параллельно горизонту).
Время нахождения тела в воздухе можно вычислить, приравняв к нулю координату y. Имеем:
0 = h+v0*sin(θ)*t-g*t2/2
Это квадратное уравнение решаем через дискриминант, получаем:
D = b2 - 4*a*c = v02*sin2(θ) - 4*(-g/2)*h = v02*sin2(θ) + 2*g*h,
t = (-b±√D)/(2*a) = (-v0*sin(θ)±√(v02*sin2(θ) + 2*g*h))/(-2*g/2) =
= (v0*sin(θ)+√(v02*sin2(θ) + 2*g*h))/g.
В последнем выражении один корень со знаком минуса отброшен, в виду его незначительного физического значения. Подставив время полета t в выражение для x, получаем дальность полета l:
l = x = v0*cos(θ)*(v0*sin(θ)+√(v02*sin2(θ) + 2*g*h))/g.
Проще всего это выражение проанализировать, если начальная высота равна нулю (h=0), тогда получим простую формулу:
l = v 02*sin(2*θ)/g
Это выражение свидетельствует, что максимальную дальность полета можно получить, если тело бросить под углом 45o (sin(2*45o) = м1).
Максимальная высота подъема тела
Помимо дальности полета, также полезно найти высоту над землей, на которую может подняться тело. Поскольку этот тип движения описывается параболой, ветви которой направлены вниз, то максимальная высота подъема является ее экстремумом. Последний рассчитывается путем решения уравнения для производной по t для y:
dy/dt = d(h+v0*sin(θ)*t-g*t2/2)/dt = v0*sin(θ)-gt=0 =>
=> t = v0*sin(θ)/g.
Подставляем это время в уравнение для y, получаем:
y = h+v0*sin(θ)*v0*sin(θ)/g-g*(v0*sin(θ)/g)2/2 = h + v02*sin2(θ)/(2*g).
Это выражение свидетельствует, что на максимальную высоту тело поднимется, если его бросить вертикально вверх (sin2(90o) = 1).