Допущения, воплощенные в статистическом моделировании, описывают набор вероятностных распределений, некоторые из которых, как предполагается, адекватно приближают распределение. Из определения отбирается конкретный набор данных. Распределения вероятностей, присущие статистическому моделированию, - это то, что отличает статистические модели от других, не статистических, математических моделей.
Связь с математикой
Этот научный метод коренится, прежде всего, в математике. Статистическое моделирование систем обычно задается математическими уравнениями, которые связывают одну или несколько случайных величин и, возможно, других неслучайных переменных. Таким образом, статистическая модель является «формальным представлением теории» (Герман Адер, цитируя Кеннета Боллена).
 Вам будет интересно:«Форсировать события»: что подразумевает фраза?
Вам будет интересно:«Форсировать события»: что подразумевает фраза?
Все статистические проверки гипотез и все статистические оценки получены из статистических моделей. В более общем смысле, статистические модели являются частью основы статистического вывода.
Методы статистического моделирования
 Вам будет интересно:Как по-английски будет «встреча»: перевод слова
Вам будет интересно:Как по-английски будет «встреча»: перевод слова
Неформально статистическая модель может рассматриваться как статистическое допущение (или набор статистических допущений) с определенным свойством: это допущение позволяет нам вычислять вероятность любого события. В качестве примера рассмотрим пару обычных шестигранных кубиков. Мы будем изучать два различных статистических предположения о кости.
Первое статистическое предположение составляет статистическую модель, потому что только с одним допущением мы можем вычислить вероятность любого события. Альтернативное статистическое допущение не составляет статистической модели, потому что только с одним допущением мы не можем рассчитать вероятность каждого события.
В приведенном выше примере с первым допущением вычислить вероятность события легко. Однако в некоторых других примерах расчет может быть сложным или даже непрактичным (например, это может потребовать миллионов лет вычислений). Для предположения, составляющего статистическую модель, такая трудность является приемлемой: выполнение вычисления не должно быть практически осуществимым, просто теоретически возможным.
Примеры моделей
 Вам будет интересно:Как научить ребенка делению: основные принципы, простые способы решения и советы учителей
Вам будет интересно:Как научить ребенка делению: основные принципы, простые способы решения и советы учителей
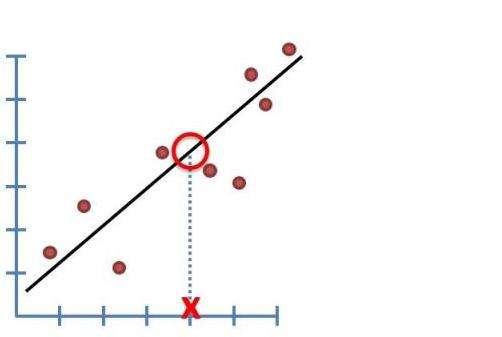
Предположим, что у нас есть популяция школьников с равномерно распределенными по возрасту детьми. Рост ребенка будет стохастически связан с возрастом: например, когда мы знаем, что ребенку 7 лет, это влияет на вероятность того, что ребенок будет ростом 5 футов (примерно 152 см). Мы могли бы формализовать эту взаимосвязь в модели линейной регрессии, например: рост = b0 + b1agei + εi, где b0 - пересечение, b1 - параметр, на который умножается возраст при получении прогноза роста, εi - термин ошибки. Это подразумевает, что рост предсказывается возрастом с некоторой ошибкой.
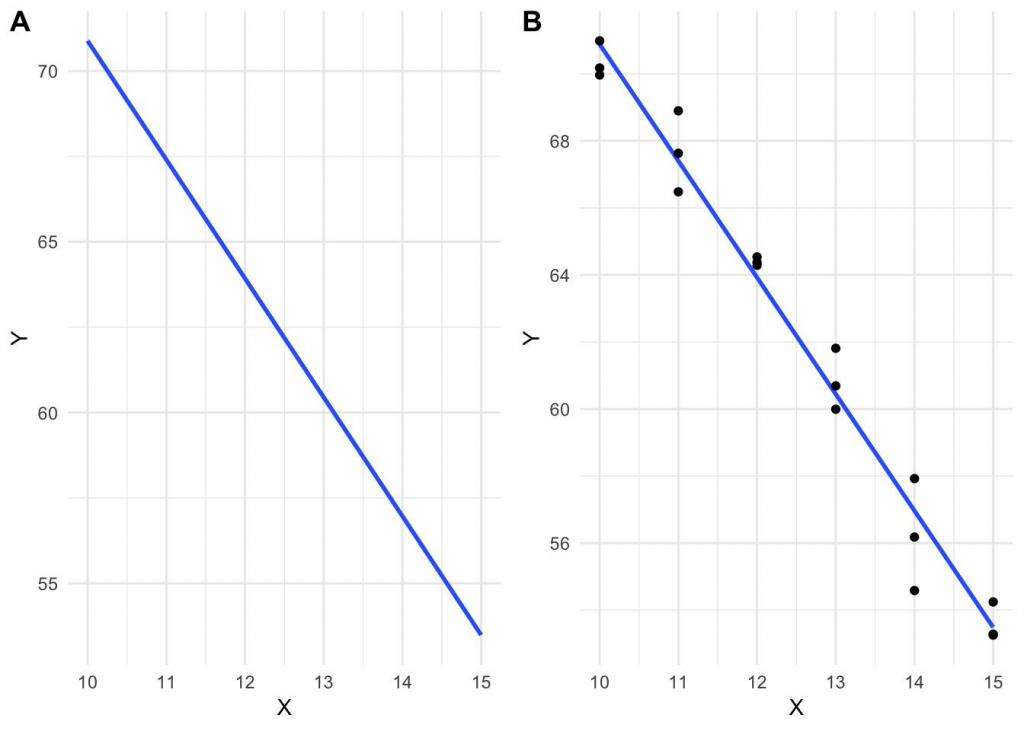
Допустимая модель должна соответствовать всем точкам данных. Таким образом, прямая линия (heighti = b0 + b1agei) не может быть уравнением для модели данных - если только она точно не соответствует всем точкам данных, то есть все точки данных идеально лежат на линии. Член ошибки εi должен быть включен в уравнение, чтобы модель соответствовала всем точкам данных.
Чтобы сделать статистический вывод, нам сначала необходимо принять некоторые вероятностные распределения для εi. Например, мы можем предположить, что распределения εi являются Гауссовскими, с нулевым средним параметром. В этом случае модель будет иметь 3 параметра: b0, b1 и дисперсию распределения Гаусса.
Общее описание
Статистическая модель - это особый класс математической модели. Что отличает статистическую модель от других математических моделей, так это то, что она недетерминирована. С ее помощью осуществляется моделирование статистических данных. Таким образом, в статистической модели, определенной с помощью математических уравнений, некоторые переменные не имеют конкретных значений, а вместо этого имеют распределения вероятностей; то есть некоторые переменные являются стохастическими. В приведенном выше примере ε является стохастической переменной; без этой переменной модель была бы детерминированной.
Статистические модели часто используются в статистическом анализе и моделировании, даже если моделируемый физический процесс является детерминированным. Например, подбрасывание монет в принципе является детерминированным процессом; все же это обычно моделируется как стохастический (через процесс Бернулли).
Параметрические модели
Параметрические модели являются наиболее часто используемыми статистическими моделями. Что касается полупараметрических и непараметрических моделей, сэр Дэвид Кокс сказал: «Как правило, они включают меньше предположений о структуре и форме распределения, но обычно содержат сильные предположения о независимости». Как и все прочие упомянутые модели, также часто используются в статистическом методе математического моделирования.
Многоуровневые модели
Многоуровневые модели (так же известные, как иерархические линейные модели, модели с вложенными данными, смешанные модели, случайные коэффициенты, модели со случайными эффектами, модели со случайными параметрами или модели с разделением на участки) являются статистическими моделями параметров, которые варьируются на более чем одном уровне. Примером может служить модель успеваемости учащихся, которая содержит показатели для отдельных учащихся, а также показатели для классных комнат, в которые сгруппированы студенты. Эти модели можно рассматривать как обобщения линейных моделей (в частности, линейной регрессии), хотя они также могут распространяться на нелинейные модели. Эти модели стали намного популярнее после того, как стали доступны достаточные вычислительные мощности и программное обеспечение.
Многоуровневые модели особенно подходят для исследовательских проектов, где данные для участников организованы на более чем одном уровне (то есть, вложенные данные). Единицами анализа обычно являются отдельные лица (на более низком уровне), которые вложены в контекстные / совокупные единицы (на более высоком уровне). В то время как самый низкий уровень данных в многоуровневых моделях, как правило, индивидуальный, повторные измерения отдельных лиц также могут быть рассмотрены. Таким образом, многоуровневые модели предоставляют альтернативный тип анализа для одномерного или многомерного анализа повторных измерений. Индивидуальные различия в кривых роста могут быть рассмотрены. Кроме того, многоуровневые модели могут использоваться в качестве альтернативы ANCOVA, где баллы по зависимой переменной корректируются для ковариат (например, индивидуальных различий) перед тестированием различий в лечении. Многоуровневые модели способны анализировать эти эксперименты без предположения об однородности наклонов регрессии, что требуется ANCOVA.
Многоуровневые модели можно использовать для данных со многими уровнями, хотя двухуровневые модели являются наиболее распространенными, и остальная часть этой статьи посвящена только этим. Зависимая переменная должна быть исследована на самом низком уровне анализа.
Выбор модели
Выбор модели - это задача выбора из набора моделей-кандидатов с учетом данных, осуществляемая в рамках статистического моделирования. В простейших случаях рассматривается уже существующий набор данных. Тем не менее задача может также включать планирование экспериментов таким образом, чтобы собранные данные хорошо подходили для задачи выбора модели. Учитывая модели-кандидаты с аналогичной предсказательной или объяснительной силой, простейшая модель, скорее всего, будет лучшим выбором (бритва Оккама).
Представители компании Konishi & Kitagawa заявляют: «Большинство проблем статистического вывода можно считать проблемами, связанными со статистическим моделированием». Аналогичным образом, Кокс сказал: «Как осуществляется перевод предметной проблемы в статистическую модель, часто является наиболее важной частью анализа».
Выбор модели может также относиться к проблеме выбора нескольких репрезентативных моделей из большого набора вычислительных моделей для целей принятия решений или оптимизации в условиях неопределенности.
Графические модели
Графическая модель, или вероятностная графическая модель, (PGM) или структурированная вероятностная модель, - это вероятностная модель, для которой график выражает структуру условной зависимости между случайными величинами. Они обычно используются в теории вероятностей, статистике (особенно в байесовской статистике), и в машинном обучении.
Эконометрические модели
Эконометрические модели - это статистические модели, используемые в эконометрике. Эконометрическая модель определяет статистические отношения, которые, как полагают, существуют между различными экономическими величинами, относящимися к конкретному экономическому явлению. Эконометрическая модель может быть получена из детерминированной экономической модели, учитывающей неопределенность, или из экономической модели, которая сама является стохастической. Тем не менее также можно использовать эконометрические модели, которые не привязаны к какой-либо конкретной экономической теории.