В чем заключается закон распределения Пирсона? Ответ на этот широкий вопрос не может быть простым и лаконичным. Система Пирсона была изначально разработана для моделирования видимых искаженных наблюдений. В то время было хорошо известно, как настроить теоретическую модель, чтобы она соответствовала двум первым кумулянтам или моментам наблюдаемых данных: любое распределение вероятностей может быть непосредственно расширено, чтобы сформировать группу масштабов местоположения.
Гипотеза Пирсона о нормальном распределении критериев
Вам будет интересно:Ученый Алексей Яблоков: биография и вклад в экологию
За исключением патологических случаев, шкала местоположения может быть сделана так, чтобы она соответствовала наблюдаемому среднему значению (первый кумулянт) и дисперсии (второй кумулянт) произвольным образом. Однако не было известно, как построить распределения вероятностей, в которых асимметрию (стандартизированный третий кумулянт) и эксцесс (стандартизированный четвертый кумулянт) можно было регулировать одинаково свободно. Эта необходимость стала очевидной при попытке подгонки известных теоретических моделей к наблюдаемым данным, которые демонстрировали асимметрию.
Вам будет интересно:1 баррель. Сколько баррелей в тонне? Что такое баррель?
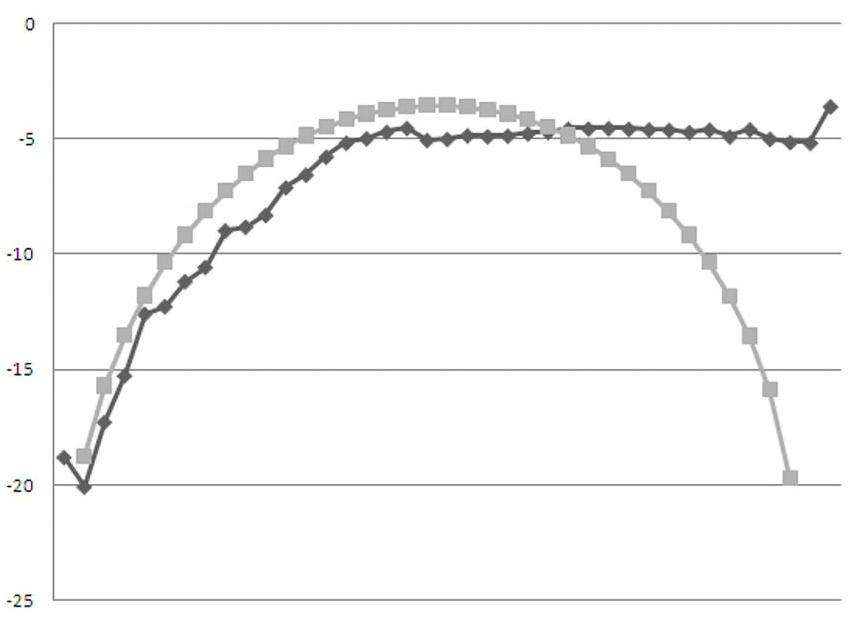
На видео ниже вы можете ознакомиться с анализом хи-распределения Пирсона.
История
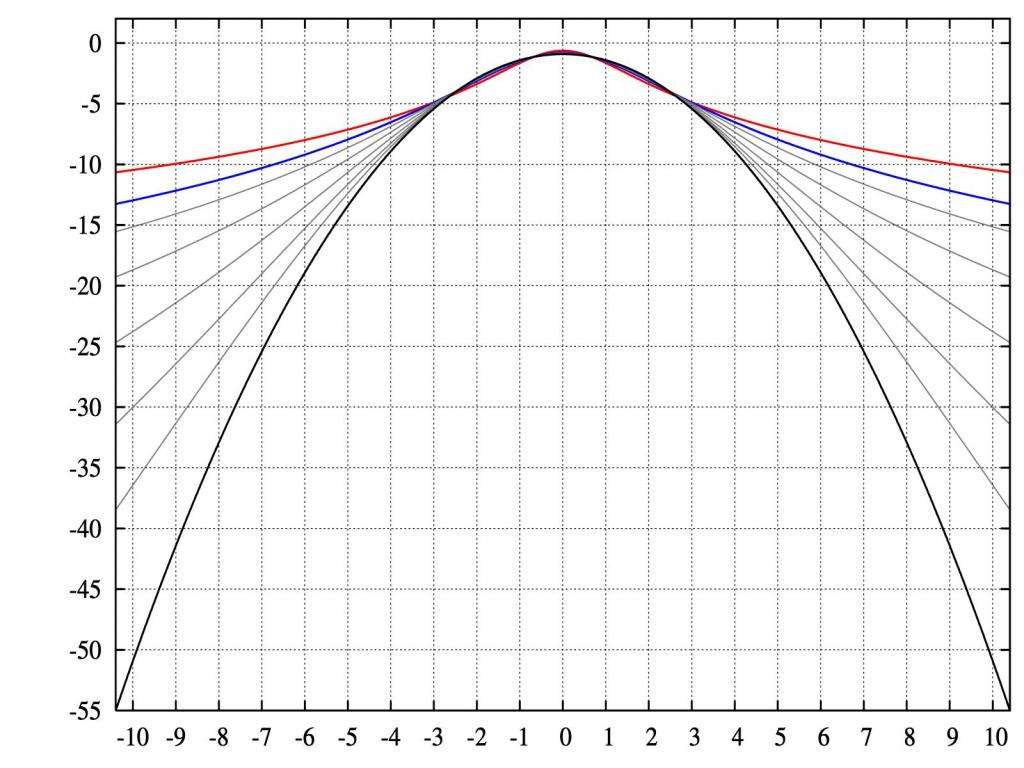
В своей оригинальной работе Пирсон выделил четыре типа распределений (пронумерованных от I до IV) в дополнение к нормальному распределению (которое первоначально было известно как тип V). Классификация зависит от того, поддерживаются ли распределения на ограниченном интервале, на полуоси или на всей реальной линии, и были ли они потенциально перекошены или обязательно симметричны.
Во второй статье были исправлены два упущения: он переопределил распределение типа V (первоначально это было только нормальное распределение, но теперь с обратной гаммой) и ввел распределение типа VI. Вместе первые две статьи охватывают пять основных типов системы Пирсона (I, III, IV, V и VI). В третьей статье Пирсон (1916) представил дополнительные подтипы.
Усовершенствование концепции
Вам будет интересно:Основные коммуникативные ситуации: определение и характеристика
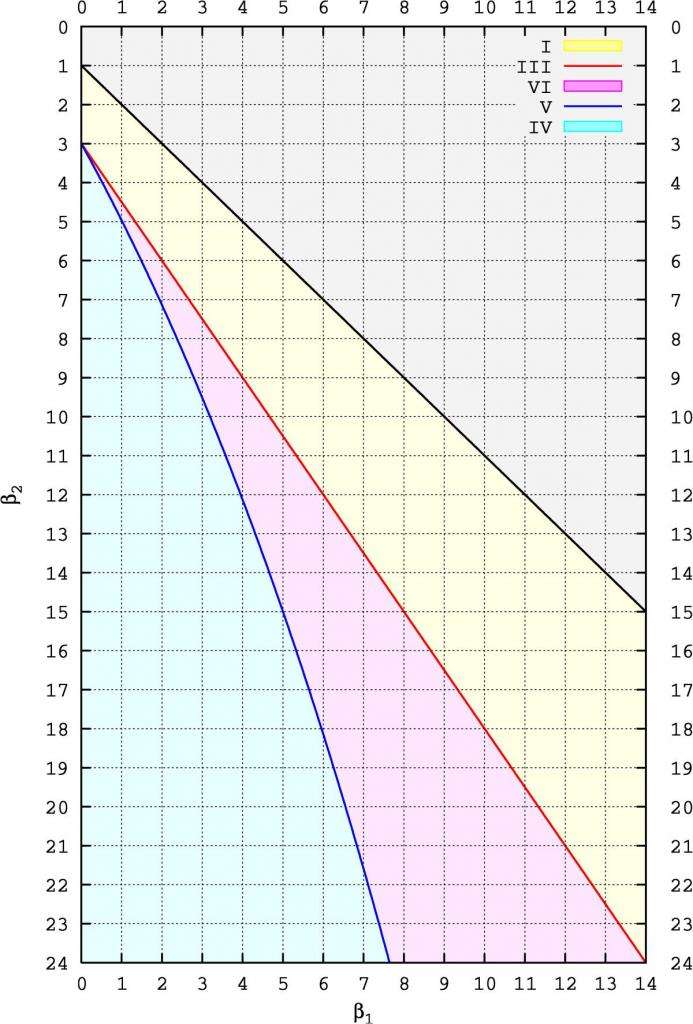
Ринд изобрел простой способ визуализации пространства параметров системы Пирсона (или распределение критериев), который был впоследствии им и принят. Сегодня этим методом пользуются очень многие математики и статисты. Типы распределений Пирсона характеризуются двумя величинами, обычно называемыми β1 и β2. Первый - это квадрат асимметрии. Вторым является традиционный эксцесс, или четвертый стандартизированный момент: β2 = γ2 + 3.
Современные математические методы определяют эксцесс γ2 в виде кумулянтов вместо моментов, так что для нормального распределения мы имеем γ2 = 0 и β2 = 3. Здесь стоит следовать историческому прецеденту и использовать β2. Диаграмма справа показывает, к какому типу относится конкретное распределение Пирсона (обозначенное точкой (β1, β2).
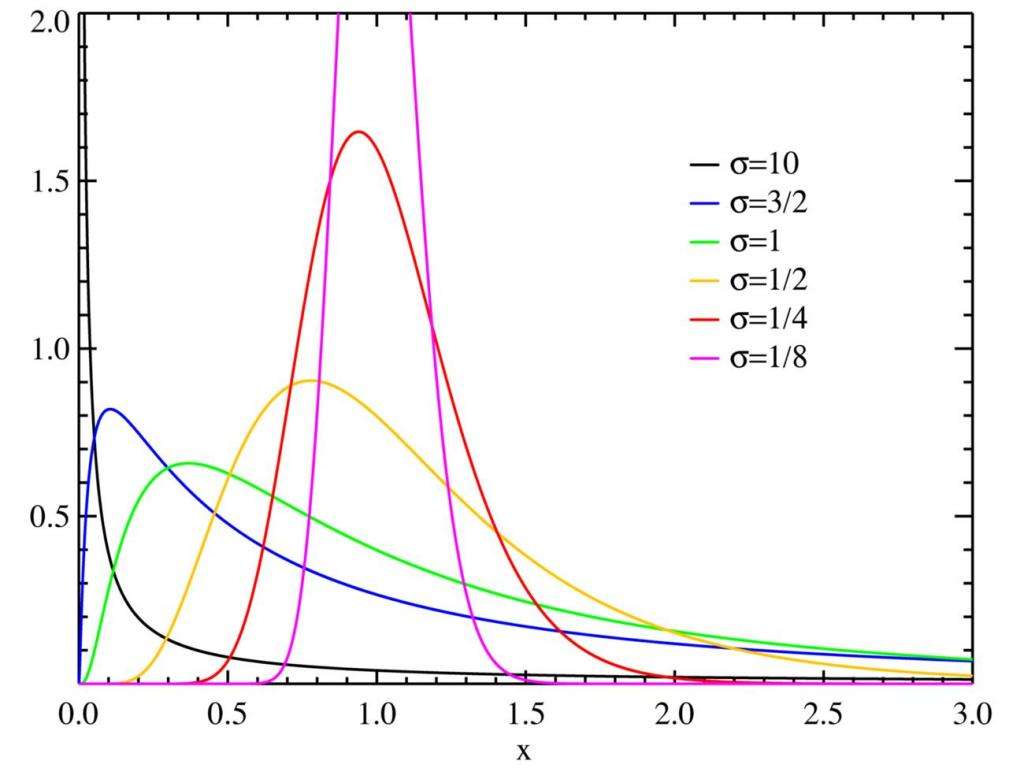
Многие из искаженных и/или немезокуртических распределений, знакомых нам сегодня, были еще не известны в начале 1890-х годов. То, что сейчас известно как бета-распределение, было использовано Томасом Байесом в качестве апостериорного параметра распределения Бернулли в его работе 1763 года об обратной вероятности.
Бета-дистрибутив приобрел известность благодаря своему присутствию в системе Пирсона и был известен до 1940-х годов как распределение Пирсона I типа. Дистрибутив типа II является частным случаем типа I, но обычно его больше не выделяют.
Гамма-распределение возникло из его же работы и было известно как нормальное распределение Пирсона III типа, прежде чем приобрело свое современное название в 1930-х и 1940-х годах. В статье ученого за 1895 год было представлено распределение типа IV, которое содержит t-распределение Стьюдента, как особый случай, предшествующий последующему использованию Уильяма Сили Госсета на несколько лет. В его статье 1901 года было представлено распределение с обратной гаммой (тип V) и бета-простых чисел (тип VI).
Другое мнение
Согласно Орду, Пирсон разработал основную форму уравнения (1) на основе формулы для производной логарифма функции плотности нормального распределения (которая дает линейное деление на квадратичную структуру). Проверкой гипотезы о распределении критериев Пирсона до сих пор занимаются многие специалисты. И она подтверждает свою эффективность.
Кем был Карл Пирсон
Карл Пирсон был английским математиком и биостатистом. Ему приписывают создание дисциплины математической статистики. В 1911 году он основал первое в мире отделение статистики в Университетском колледже Лондона и внес значительный вклад в области биометрии и метеорологии. Пирсон был также сторонником социального дарвинизма и евгеники. Он был протеже и биографом сэра Фрэнсиса Гальтона.
Биометрия
Карл Пирсон сыграл важную роль в создании школы биометрии, которая была конкурирующей теорией для описания эволюции и наследования населения на рубеже 20-го века. Его серия из восемнадцати работ «Математический вклад в теорию эволюции» утвердила его как основателя биометрической школы наследования. Фактически Пирсон посвятил много времени в течение 1893-1904 гг. разработке статистических методов для биометрии. Эти методы, которые широко используются сегодня для статистического анализа, включают критерий хи-квадрата, стандартное отклонение, коэффициенты корреляции и регрессии.
Вопрос наследственности
Закон наследственности Пирсона гласил, что зародышевая плазма состоит из элементов, унаследованных от родителей, а также от более далеких предков, доля которых варьировалась по разным признакам. Карл Пирсон был последователем Гальтона, и хотя их работы отличались в некоторых отношениях, Пирсон использовал значительное количество статистических концепций своего учителя в формулировке биометрической школы для наследования, такой как закон регрессии.
Особенности школы
Биометрическая школа, в отличие от менделевцев, была сосредоточена не на обеспечении механизма наследования, а на предоставлении математического описания, которое не было причинно-следственным по своей природе. В то время как Гальтон предложил прерывистую теорию эволюции, в которой виды должны были бы изменяться посредством больших скачков, а не небольших изменений, которые накапливались со временем, Пирсон указал на недостатки в этом аргументе и фактически использовал его идеи для развития непрерывной теории эволюции. Менделевцы предпочитали прерывистую теорию эволюции.
В то время как Гальтон сосредоточился главным образом на применении статистических методов к изучению наследственности, Пирсон и его коллега Уэлдон расширили рассуждения в этой области, вариации, корреляции естественного и полового отбора.
Взгляд на эволюцию
Для Пирсона теория эволюции не предназначалась для идентификации биологического механизма, объясняющего закономерности наследования, тогда как менделевский подход объявлял ген механизмом наследования.
Пирсон раскритиковал Бейтсона и других биологов за то, что они не приняли биометрические методы в своем исследовании эволюции. Он осуждал ученых, которые не сосредоточились на статистической достоверности своих теорий, заявив:
«Прежде чем мы сможем принять [любую причину прогрессивного изменения] в качестве фактора, мы должны не только показать его правдоподобие, но, если возможно, продемонстрировать его количественную способность».
Биологи уступили «почти метафизическим предположениям о причинах наследственности», которые заменили процесс сбора экспериментальных данных, что на самом деле способно позволить ученым сузить потенциальные теории.
Законы природы
Для Пирсона законы природы были полезны для точных прогнозов и для краткого описания тенденций в наблюдаемых данных. Причиной был опыт, «что определенная последовательность произошла и повторилась в прошлом».
Таким образом, выявление конкретного механизма генетики не было достойным занятием биологов, которые должны вместо этого сосредоточиться на математических описаниях эмпирических данных. Это отчасти привело к ожесточенным спорам между биометристами и менделианцами, включая Бейтсона.
После того как последний отверг одну из рукописей Пирсона, описывающую новую теорию изменчивости потомства или гомотипии, Пирсон и Уэлдон основали компанию Biometrika в 1902 году. Хотя биометрический подход к наследованию в конечном итоге утратил менделевский взгляд, методы, которые они в то время разработали, жизненно важны для изучения биологии и эволюции сегодня.
