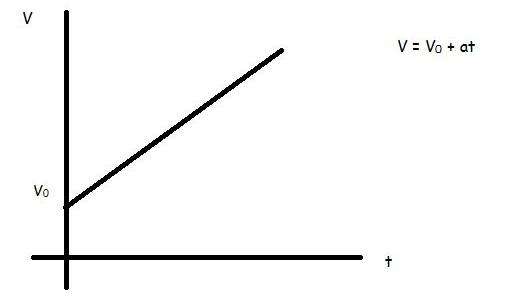Изучением классического механического движения в физике занимается кинематика. В отличие от динамики, наука изучает, почему движутся тела. Она отвечает на вопрос, как они это делают. В данной статье рассмотрим, что такое ускорение и движение с постоянным ускорением.
Понятие об ускорении
Когда тело движется в пространстве, за некоторое время оно преодолевает определенный путь, который является длиной траектории. Чтобы рассчитать этот путь, пользуются понятиями скорости и ускорения.
Скорость как физическая величина характеризует быстроту во времени изменения пройденного пути. Скорость направлена по касательной к траектории в сторону перемещения тела.
 Вам будет интересно:Распределение Пирсона: определение, применение
Вам будет интересно:Распределение Пирсона: определение, применение
Ускорение — это несколько более сложная величина. Говоря кратко, она описывает изменение скорости в рассматриваемый момент времени. Математическое определение ускорения выглядит так:
a¯ = dv¯/dt.
Чтобы яснее понять эту формулу, приведем простой пример: предположим, что за 1 секунду движения скорость тела увеличилась на 1 м/с. Эти цифры, подставленные в выражение выше, приводят к результату: ускорение тела в течение этой секунды было равно 1 м/с2.
Направление ускорения совершенно не зависит от направления скорости. Его вектор совпадает с вектором результирующей силы, которая вызывает это ускорение.
Следует отметить важный момент в приведенном определении ускорения. Эта величина характеризует не только изменение скорости по модулю, но и по направлению. Последний факт следует учитывать в случае криволинейного движения. Далее в статье будет рассматриваться только прямолинейное движение.
Скорость при движении с постоянным ускорением
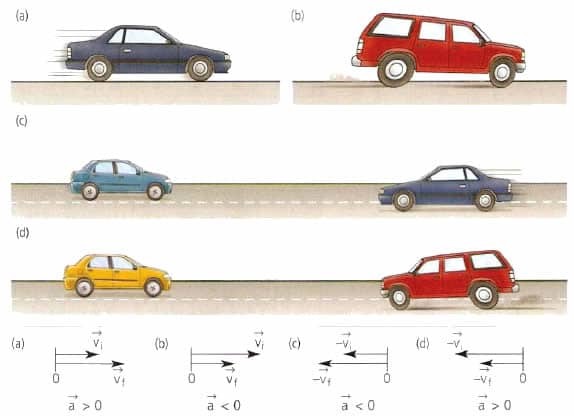
Ускорение является постоянным, если оно в процессе движения сохраняет свой модуль и направление. Такое движение называют равноускоренным или равнозамедленным — все зависит от того, приводит ли ускорение к увеличению скорости или к ее уменьшению.
В случае движения тела с постоянным ускорением определить скорость можно по одной из следующих формул:
v = a*t;
v = v0 + a*t;
v = v0 - a*t.
Первые два уравнения характеризуют равноускоренное перемещение. Отличие между ними заключается в том, что второе выражение применимо для случая ненулевой начальной скорости.
Третье уравнение — это выражение для скорости при равнозамедленном движении с постоянным ускорением. Ускорение при этом направлено против скорости.
Графиками всех трех функций v(t) являются прямые. В первых двух случаях прямые имеют положительный наклон относительно оси абсцисс, в третьем случае этот наклон является отрицательным.
Формулы пройденного пути
Для пути в случае движения с ускорением постоянным (ускорение a = const) получить формулы несложно, если вычислить интеграл от скорости по времени. Проделав эту математическую операцию для записанных выше трех уравнений, мы получим следующие выражения для пути L:
L = a*t2/2;
L = v0*t + a*t2/2;
L = v0*t - a*t2/2.
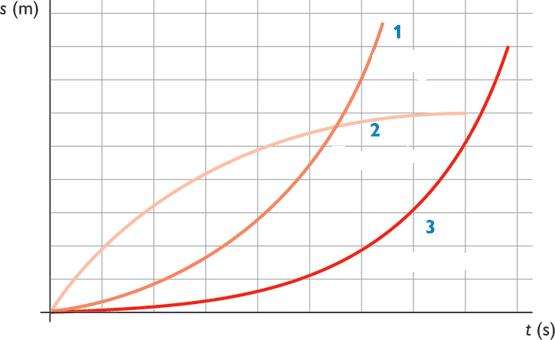
Графиками всех трех функций пути от времени являются параболы. В первых двух случаях правая ветвь параболы возрастает, а для третьей функции она постепенно выходит на некоторую константу, которая соответствует пройденному пути до полной остановки тела.
Решение задачи
Двигаясь со скоростью 30 км/ч, автомобиль начал ускоряться. За 30 секунд он прошел расстояние 600 метров. Чему было равно ускорение автомобиля?
В первую очередь переведем начальную скорость из км/ч в м/с:
v0 = 30 км/ч = 30000/3600 = 8,333 м/с.
Теперь запишем уравнение движения:
L = v0*t + a*t2/2.
Из этого равенства выразим ускорение, получим:
a = 2*(L - v0*t)/t2.
Все физические величины в этом уравнении известны из условия задачи. Подставляем их в формулу и получаем ответ: a ≈ 0,78 м/с2. Таким образом, двигаясь с ускорением постоянным, автомобиль за каждую секунду увеличивал свою скорость на 0,78 м/с.
Рассчитаем также (для интереса), какую скорость он приобрел через 30 секунд ускоренного движения, получаем:
v = v0 + a*t = 8,333 + 0,78*30 = 31,733 м/с.
Полученная скорость равна 114,2 км/ч.