Кинематика - это часть физики, которая рассматривает законы движения тел. Ее отличие от динамики заключается в том, что она не рассматривает действующие на передвигающееся тело силы. Данная статья посвящена вопросу о кинематике вращательного движения.
Вращательное движение и его отличие от поступательного
Если обратить внимание на окружающие передвигающиеся предметы, то можно заметить, что они либо перемещаются по прямой линии (автомобиль едет по дороге, самолет летит по небу), либо по окружности (тот же автомобиль, входящий в поворот, вращение колеса). Более сложные виды движения объектов можно свести в первом приближении к комбинации отмеченных двух типов.
Вам будет интересно:Обучение в Колледже транспорта в Тюмени
Поступательное перемещение предполагает изменение пространственных координат тела. При этом оно часто рассматривается как материальная точка (геометрические размеры не принимаются во внимание).
Вращательное движение - это такой тип перемещения, при котором система движется по окружности вокруг некоторой оси. Причем предмет в этом случае редко рассматривается как материальная точка, чаще всего используют другое приближение - абсолютно твердое тело. Последнее означает, что силами упругости, действующими между атомами тела, пренебрегают и считают, что при вращении геометрические размеры системы не изменяются. Наиболее простым случаем является неподвижная ось.
Вам будет интересно:Староста группы: Обязанности, права, привилегии
Кинематика поступательного и вращательного движения подчиняется одним и тем же законам Ньютона. Для описания обоих видов перемещения используют подобные физические величины.
Какие величины описывают движение в физике?
Кинематика вращательного и поступательного движения использует три основные величины:
Также часто используют понятие траектории. Но для рассматриваемых типов перемещения объектов это понятие становится тривиальным, поскольку поступательное движение характеризуется линейной траекторией, а вращательное - окружностью.
Линейная и угловая скорости
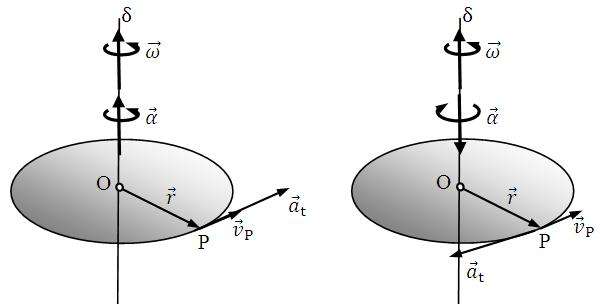
Кинематику вращательного движения материальной точки начнем рассматривать с понятия скорости. Известно, что для поступательного перемещения тел эта величина описывает, какой путь будет преодолен за единицу времени, то есть:
v = L / t
Величина v измеряется в метрах в секунду. Для вращения неудобно рассматривать эту линейную скорость, поскольку она зависит от расстояния до оси вращения. Вводят несколько иную характеристику:
ω = θ / t
Эта одна из главных формул кинематики вращательного движения. Она показывает, на какой угол θ повернется вся система вокруг неподвижной оси за время t.
Обе приведенные формулы отражают один и тот же физический процесс быстроты перемещения. Только для линейного случая важное значение имеет расстояние, а для кругового - угол поворота.
Обе формулы взаимодействуют друг с другом. Получим эту связь. Если выражать θ в радианах, тогда материальная точка, вращающаяся на расстоянии R от оси, совершив один оборот, пройдет путь L = 2 * pi * R. Выражение для линейной скорости примет вид:
v = L / t = 2 * pi * R / t
Но ведь отношение 2 * pi радиан ко времени t - это не что иное, как угловая скорость. Тогда получаем:
v = ω * R
Отсюда видно, что чем больше линейная скорость v и меньше радиус вращения R, тем больше скорость угловая ω.
Линейное и угловое ускорение
Другой важной характеристикой в кинематике вращательного движения материальной точки является угловое ускорение. Перед тем как познакомиться с ним, приведем формулу для аналогичной линейной величины:
1) a = dv / dt
2) a = Δv / Δt
Первое выражение отражает мгновенное ускорение (dt -> 0), вторую же формулу уместно применять, если скорость изменяется равномерно за время Δt. Полученное во втором варианте ускорение называют средним.
Учитывая подобие величин, которые описывают линейное и вращательное движение, для углового ускорения можно записать:
1) α = dω / dt
2) α = Δω / Δt
Интерпретация этих формул точно такая же, как и для линейного случая. Единственное отличие заключается в том, что a показывает, на сколько метров в секунду изменяется скорость за единицу времени, а α - на сколько радиан в секунду изменяется угловая скорость за тот же период времени.
Найдем связь между этими ускорениями. Подставив значение для v, выраженной через ω, в любое из двух равенств для α, получим:
α = Δω / Δt = Δv / Δt*1 / R = a / R
Отсюда следует, что чем меньше радиус вращения и больше линейное ускорение, тем больше будет величина α.
Пройденный путь и угол поворота
Осталось привести формулы для последней из трех основных величин в кинематике вращательного движения вокруг неподвижной оси - для угла поворота. Как и в предыдущих пунктах, сначала запишем формулу для равномерно ускоренного прямолинейного перемещения, имеем:
L = v0 * t + a * t2 / 2
Полная аналогия с вращательным движением приводит к следующей формуле для него:
θ = ω0 * t + α * t2 / 2
Последнее выражение позволяет получить угол поворота за любое время t. Заметим, что окружность составляет 2 * pi радиан (≈ 6,3 радиана). Если в результате решения задачи получается значение θ больше, чем указанная величина, значит, тело совершило больше одного оборота вокруг оси.
Формулу связи L и θ получим, подставляя соответствующие значения для ω0 и α через линейные характеристики:
θ = v0 * t / R + a * t2 / (2 * R) = L /R
Полученное выражение отражает смысл самого угла θ в радианах. Если θ = 1 рад, тогда L = R, то есть угол в один радиан опирается на дугу длиною в один радиус.
Пример решения задачи
Решим следующую проблему кинематики вращательного движения: известно, что машина движется со скоростью 70 км/ч. Зная, что диаметр его колеса равен D = 0,4 метра, необходимо определить величину ω для него, а также количество оборотов, которые оно сделает, когда автомобиль проедет путь в 1 километр.
Чтобы найти угловую скорость, достаточно подставить известные данные в формулу связи ее со скоростью линейной, получаем:
ω = v / R = 7 * 104 / 3600 / 0,2 = 97,222 рад/с.
Аналогично для угла θ, на который повернется колесо, пройдя 1 км, получаем:
θ = L / R = 1000 / 0,2 = 5000 рад.
Учитывая, что один оборот составляет 6,2832 радиана, получаем число оборотов колеса, которое этому углу соответствует:
n = θ / 6,2832 = 5000 / 6,2832 = 795,77 оборотов.
Мы ответили на вопросы, используя приведенные в статье формулы. Также можно было решить задачу иным способом: вычислить время, за которое автомобиль проедет 1 км, и подставить его в формулу для угла поворота, откуда и получить угловую скорость ω. Ответ найден.