Призма является одной из известных фигур, изучаемых в курсе стереометрии в общеобразовательных школах. Чтобы уметь рассчитывать различные характеристики для фигур этого класса, необходимо знать, какие виды призм существуют. Рассмотрим этот вопрос подробнее.
Призма в стереометрии
В первую очередь дадим определение упомянутому классу фигур. Призмой является любой многогранник, состоящий из двух параллельных многоугольных оснований, которые между собой соединены параллелограммами.
 Вам будет интересно:Как называется домик для пчел? Размеры улья
Вам будет интересно:Как называется домик для пчел? Размеры улья
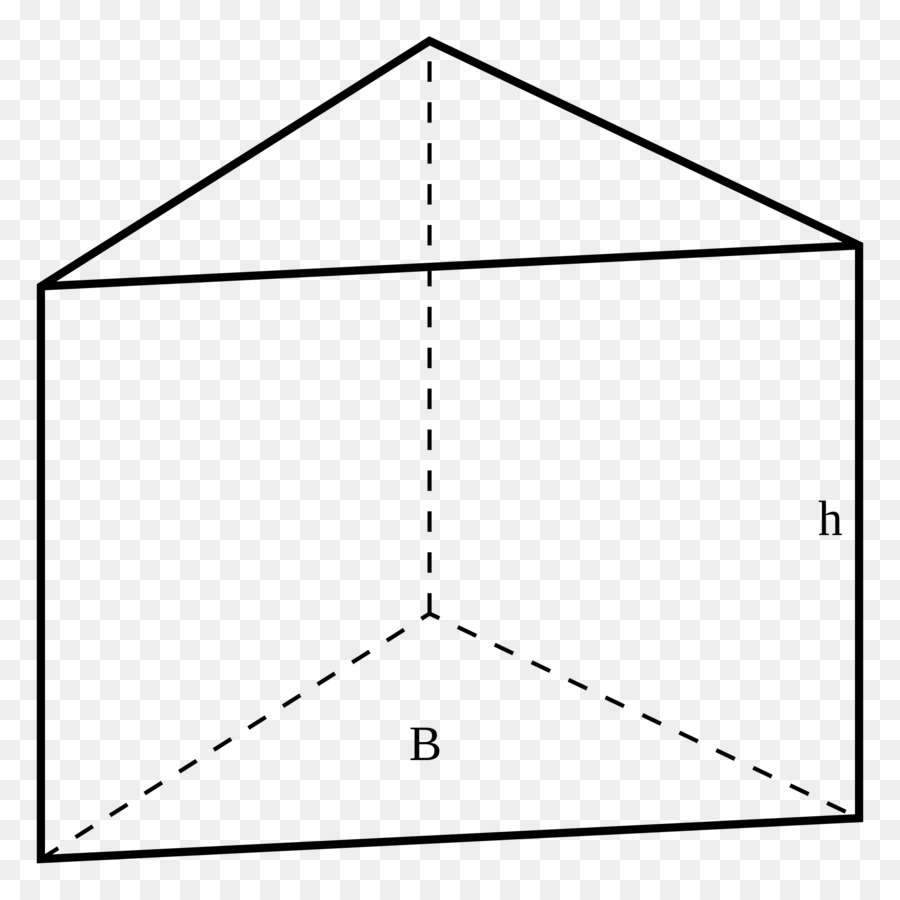
Получить эту фигуру можно так: следует выбрать произвольный многоугольник на плоскости, а затем перемещать его на длину любого вектора, который не принадлежит исходной плоскости многоугольника. В ходе такого параллельного перемещения стороны многоугольника опишут боковые грани будущей призмы, а конечное положение многоугольника станет вторым основанием фигуры. Описанным способом может быть получена произвольного вида призма. Рисунок ниже демонстрирует призму треугольную.
Каких бывают призмы видов?
Речь идет о классификации фигур рассматриваемого класса. В общем случае эту классификацию осуществляют с учетом особенностей многоугольного основания и боковых сторон фигуры. Обычно выделяют следующие три вида призм:
Призма любого из названных типов классификации может иметь четырехугольное, пятиугольное, ..., n-угольное основание. Что касается видов треугольной призмы, то она может быть классифицирована только по первым двум названным пунктам. Треугольная призма всегда является выпуклой.
Ниже подробнее рассмотрим каждый из названных типов классификации и приведем некоторые полезные формулы для вычисления геометрических свойств призмы (площади поверхности, объема).
Прямые и наклонные фигуры
Отличить прямую призму от косоугольной можно с первого взгляда. Приведем соответствующий рисунок.
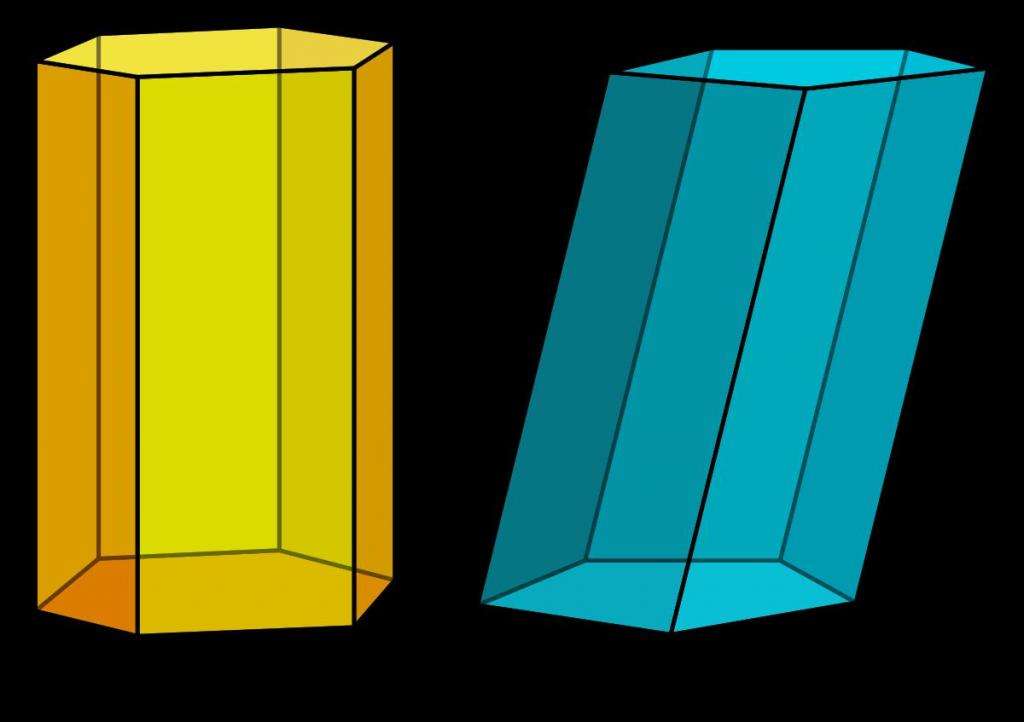
Здесь показаны две призмы (шестиугольная слева и пятиугольная справа). Каждый с уверенностью скажет, что шестиугольная является прямой, а пятиугольная - наклонной. Какой геометрический признак отличает эти призмы? Конечно же, тип боковой грани.
У прямой призмы, независимо от ее основания, все грани являются прямоугольниками. Они могут быть равны друг другу, а могут отличаться, важно лишь то, что это прямоугольники, и их двугранные углы с основаниями равны 90o.
Касательно наклонной фигуры, следует сказать, что все или некоторые боковые грани у нее являются параллелограммами, которые с основанием образуют непрямые двугранные углы.
Для всех видов прямых призм высотой является длина бокового ребра, для наклонных же фигур высота всегда меньше их боковых ребер. Знание высоты призмы важно при вычислении площади ее поверхности и объема. Например, формула объема имеет вид:
V = So*h
Где h - высота, So - площадь одного основания.
Призмы правильные и неправильные
Любая призма является неправильной, если она не прямая, или ее основание не является правильным. Вопрос прямых и наклонных призм был разобран выше. Здесь рассмотрим, что означает выражение "правильное многоугольное основание".
Многоугольник является правильным, если все его стороны равны (обозначим их длину буквой a), и все его углы также равны между собой. Примерами правильных многоугольников являются треугольник равносторонний, квадрат, шестиугольник с шестью углами по 120o и так далее. Площадь любого правильного n-угольника рассчитывается с помощью такой формулы:
Sn = n/4*a2*ctg(pi/n)
Ниже схематически показано, как выглядят правильные призмы с треугольным, квадратным, ..., восьмиугольным основаниями.
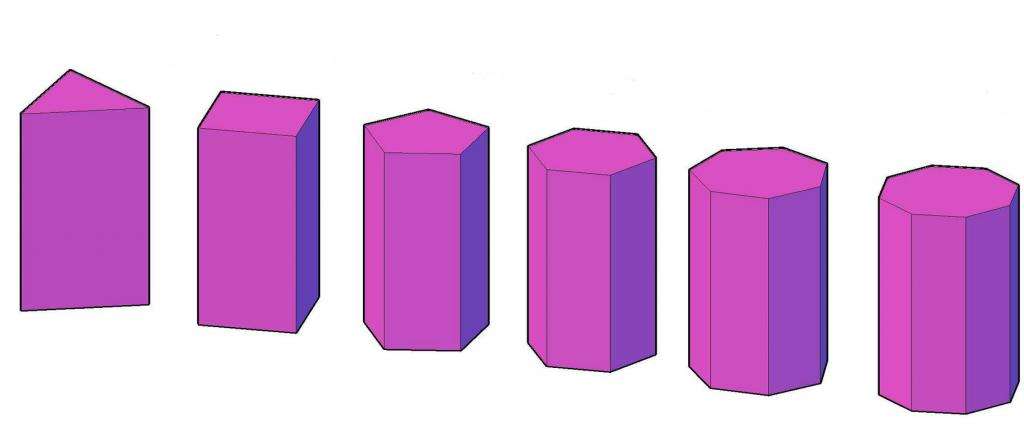
Используя записанную выше формулу для V, можно записать соответствующее выражение для правильных фигур:
V = n/4*a2*ctg(pi/n)*h
Что касается площади полной поверхности, то для правильных призм она образована площадями двух одинаковых оснований и n одинаковых прямоугольников со сторонами h и a. Указанные факты позволяют записать формулу для площади поверхности любой правильной призмы:
S = n/2*a2*ctg(pi/n) + n*a*h
Здесь первое слагаемое соответствует площади двух оснований, второе слагаемое определяет площадь исключительно боковой поверхности.
Из всех видов призм правильных лишь для четырехугольной существуют собственные названия. Так, четырехугольная призма правильная, у которой a≠h, называется прямоугольным параллелепипедом. Если же у этой фигуры a=h, то говорят о кубе.
Вогнутые фигуры
До настоящего времени мы рассматривали исключительно выпуклые виды призм. Именно им уделяется основное внимание при изучении рассматриваемого класса фигур. Тем не менее существуют также вогнутые призмы. Они от выпуклых отличаются тем, что их основания представляют собой вогнутые многоугольники, начиная с четырехугольника.

На рисунке для примера изображены две вогнутые призмы, которые изготовлены из бумаги. Левая из них в форме пятиконечной звезды является десятиугольной призмой, правая в форме шестиконечной звезды называется двенадцатиугольной вогнутой прямой призмой.