- Задания для тренировки уже имеющихся навыков и проверки знаний
- Правило постановки знаков
- Умножение одночлена на многочлен
- Умножение многочлена на многочлен
- Формулы сокращенного умножения
- Геометрический смысл
- Вопросы для самопроверки
- Упражнения по пройденной теме
- Тест: умножение многочлена на одночлен
- Заключение
Логичным началом прохождения новой темы "Многочлены" является вводный урок, освещающий тему умножения многочлена на одночлен. Для начала стоит дать основные определения, которые будут использоваться в этом уроке.
Одночлен - это простое математическое выражение, представляющее собой произведение константы на переменную или несколько переменных, взятых в целой неотрицательной степени без использования знаков + или -.
Многочлен - это сумма одночленов.
Основной задачей этого урока является выведение общего правила умножения одночлена на многочлен, а также развитие навыков для применения этого правила на практике. Обратите внимание, что знания, полученные из этой статьи, пригодятся каждому ученику в течение всего курса изучения алгебры.
 Вам будет интересно:Институт культуры в Минске: история, факультеты и особенности поступления
Вам будет интересно:Институт культуры в Минске: история, факультеты и особенности поступления
Для изучения этой темы вспомним теоретические знания, которые ученики должны получить из предыдущих уроков. Один из необходимых фрагментов теории - свойства степеней.
Задания для тренировки уже имеющихся навыков и проверки знаний
1. Необходимо определить сумму предоставленных одночленов, разность одночленов, произведение одночленов, частное одночленов и квадрат каждого из них.
2. Даны многочлены. Необходимо указать степень каждого из них. Степенью многочлена называется наивысшая степень одночлена, входящего в состав многочлена.
Решив тренировочные упражнения, можно приступить к получению новых знаний.
Правило постановки знаков
1. При умножении двух положительных (+) чисел знак произведения не меняется (+).
2. При умножении двух отрицательных (-) чисел знак произведения меняется на противоположный (+).
3. При умножении положительного (+) числа на отрицательное (-) число произведения отрицательно (-).
Одним словом, ничего сложного.
Умножение одночлена на многочлен
Используем распределительный закон умножения a * (b +c ) =a * b + a * c для решения поставленной задачи:
4x3 (3x2 – 8x + 2) = 3x2 * 4x3 - 8x * 4x3 + 2 * 4x3 = 12х5 - 32х4 + 8х3.
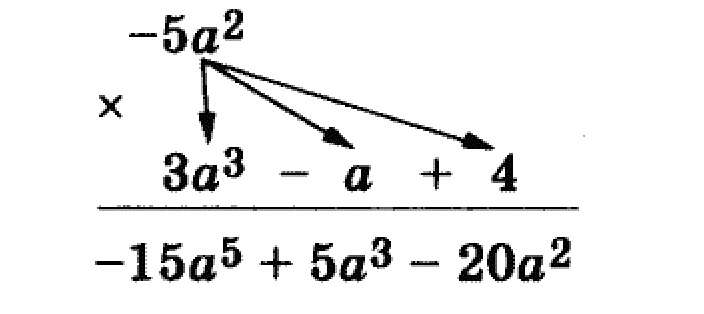
Имея знания по умножению одночлена на одночлен и умножения одночлена на число, вычислим значение данного выражения и сверим получившееся выражение с представленным выше ответом. Важно не забывать и правильно использовать правило постановки знаков.
Умножение многочлена на многочлен
Умножение многочлена на многочлен по своему алгоритму не сильно отличается от умножения одночлена на многочлен. Просто необходимо последовательно перемножить каждый одночлен из одного из многочленов на все одночлены, из которых состоит другой многочлен.
Упражнение для самопроверки:
(5xy −3 x2) * (x2 + 3y) = 5xy * x2 + 5xy * 3y - 3x2 * x2 - 3x2 * 3y = 5x3y + 15xy2 - 3x4 - 9x2y.
Вычислите произведение многочленов самостоятельно и сверьте получившееся выражение с представленным выше ответом. Важно не забывать и правильно использовать правило постановки знаков.
Формулы сокращенного умножения
Усвоив правила умножения, можно и нужно немного расширить свои знания новыми формулами, связанными с данной темой. Важно понимать, что формулы сокращенного умножения по алгебре можно вывести и самостоятельно, пользуясь распределительным свойством умножения, но на практике встречаются они довольно часто, поэтому настоятельно рекомендуется выучить эти формулы.

Необходима проверка. Вы можете самостоятельно умножить многочлен на многочлен и проверить, что после взаимного уничтожения всех вспомогательных слагаемых остаются только указанные в формулах слагаемые.
Геометрический смысл
Для упрощения понимания процесса умножения одночлена на многочлен стоит рассмотреть геометрический смысл этой математической операции.
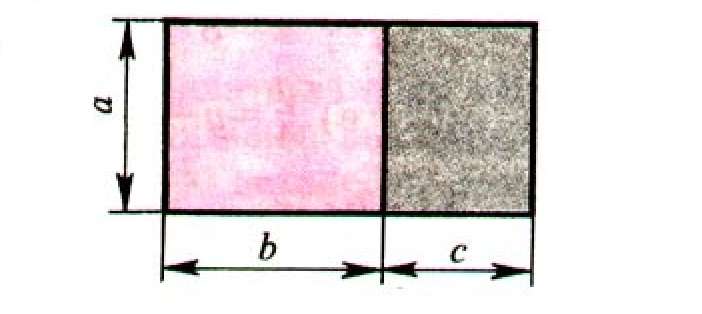
Здесь важно объяснить обучающимся на примере геометрических фигур распределительный закон умножения и тождественное равенство обеих его частей.
Вопросы для самопроверки
Упражнения по пройденной теме
1). -3х3 (х2 + 3х - 4).
2). 15x2 (xy - 4x2y2 + 4).
3). -0,7m3n (10mn – 20m2 – 3).
4). (2a4 – a3 + 0,1a) (-5a2).
5). 0,5с (3с2d – 15c3d).
6). 0,5p2 (4q – 2pq + 6p2).
7). 20xy2 (5x2y – 2,4y – 0,6).
8). 4a2b (2a – 3ab2 + 8b2).
Тест: умножение многочлена на одночлен
Для проверки полученных знаний ниже предлагается специальный тест.
| 1. Узнайте произведение: -5х (-3х + 2х2 - 2).
а) -10х3 - 15х2 + 10х. б) -10х3 + 15х2 - 10х. в) -10х3 - 15х2 + 10. г) -10х3 + 15х2 + 10х |
| 2. Замените знак (*) на выражение для получения истинного равенства:
-2х2 (*) = -8х4а2 + 4х2а - 6х4. а) 4а2х - 2а - 3х2. б) 3х2 - 2а + 4а2х2. в) 2а - 3х2 - 4а2х2. г) -4а2х2 + 3х2 + 2а |
|
3. Найдите произведение: 3а (2в - а) - 4в (в + 2а). а) 3а2 - 4b2. б) -3а2 - 2ab - 4b2. в) 3а2 + 2ab + 4b2. г) -3а2 - 4b2 |
| 4. Найдите корень заданного уравнения: 8х2 + 3х = 0.
а) х = 0. б) х = -(3/8). в) х = 0; х = (3/8). г) х = 0; х = -(3/8) |
| 5. Определите делитель данного выражения: 54 + 55 + 56.
а) 15. б) 31. в) 10. г) 55 |
Ключи к тесту: 1-г; 2-б; 3-б; 4-г; 5-б.
Заключение
На этом уроке обучающиеся получили теоретический материал с практическими примерами его применения по теме "Умножение одночлена на многочлен". А также узнали дополнительный материал, который пригодится им в дальнейшем изучении предмета. А именно, формулы сокращенного умножения по алгебре.
В процессе выполнения упражнений развивалось аналитическое мышление у обучающихся.
Обучающимися должны были быть сделаны определенные выводы о применении этой темы на практике. Умножение одночлена на многочлен применяется:
- в процессе упрощения выражений;
- в процессе нахождения корня уравнения;
- с целью доказательства некоторых тождественных выражений;
- в процессе решения задач на составление уравнений.

