Агрегатное состояние материи, в котором кинетическая энергия частиц намного превышает их потенциальную энергию взаимодействия, называется газом. Физику подобных веществ начинают рассматривать в старших классах школ. Ключевым вопросом при математическом описании этой текучей субстанции является уравнение состояния идеального газа. Изучим детально его в статье.
Идеальный газ и его отличие от реального
 Вам будет интересно:Земля Ханаанская - где она находится
Вам будет интересно:Земля Ханаанская - где она находится
Как известно, для любого газового состояния характерно хаотичное движение с разными скоростями составляющих его молекул и атомов. В реальных газах, примером которых может служить воздух, частицы так или иначе взаимодействуют друг с другом. В основном это взаимодействие носит ван-дер-ваальсовый характер. Тем не менее, если температуры газовой системы высоки (комнатная и выше), а давление не является огромным (соответствует атмосферному), то ван-дер-ваальсовые взаимодействия настолько малы, что не оказывают влияния на макроскопическое поведение всей газовой системы. В таком случае говорят об идеальном.
Собирая изложенную выше информацию в одно определение, можно сказать, что идеальный газ - это система, в которой отсутствуют взаимодействия между частицами. Сами частицы являются безразмерными, но имеют определенную массу, а столкновения частиц со стенками сосуда носят упругий характер.
Практически все газы, с которыми человек сталкивается в быту (воздух, природный метан в газовых плитах, водяной пар) можно с удовлетворительной для многих практических проблем точностью считать идеальными.
Предпосылки появления уравнения состояния идеального газа в физике
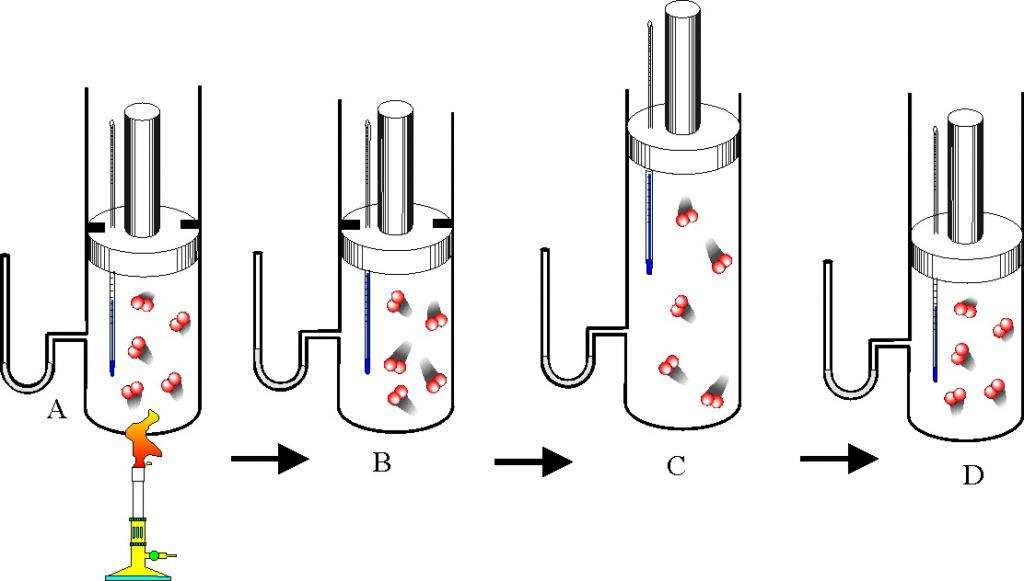
Человечество активно изучало газовое состояние вещества с научной точки зрения в течение XVII-XIX веков. Первым законом, который описал изотермический процесс, стало экспериментально открытое Робертом Бойлем и Эдмом Мариоттом следующее соотношение между объемом системы V и давлением в ней P:
- P * V = const, при T = const.
Проводя эксперименты с различными газами во второй половине XVII века, упомянутые ученые установили, что зависимость давления от объема всегда имеет вид гиперболы.
Затем в конце XVIII - в начале XIX века Французские ученые Шарль и Гей-Люссак обнаружили экспериментально еще два газовых закона, которые описывали математически изобарный и изохорный процессы. Оба закона приведены ниже:
- V / T = const, при P = const;
- P / T = const, при V = const.
Оба равенства свидетельствуют о прямой пропорциональности между объемом газа и температурой, а также между давлением и температурой при сохранении постоянного давления и объема, соответственно.
Еще одной предпосылкой для составления уравнения состояния идеального газа стало открытие Амедео Авагадро в 10-х годах XIX века следующего соотношения:
- n / V = const, при T, P = const.
Итальянец экспериментально доказал, если увеличивать количество вещества n, то при постоянных температуре и давлении объем будет линейно возрастать. Самое удивительное заключалось в том, что разные по своей природе газы при одинаковых давлениях и температурах занимали один и тот же объем, если их количество совпадало.
Закон Клапейрона-Менделеева

В 30-е годы XIX века француз Эмиль Клапейрон опубликовал работу, в которой привел уравнение состояния газа идеального. Оно немного отличалось от современной формы. В частности, Клапейрон использовал определенные константы, измеренные экспериментально его предшественниками. Спустя несколько десятилетий наш соотечественник Д. И. Менделеев заменил константы Клапейрона одной единственной - универсальной газовой постоянной R. В итоге универсальное уравнение приобрело современный вид:
- P * V = n * R * T.
Нетрудно догадаться, что это оно является простым объединением формул газовых законов, которые были записаны выше в статье.
Постоянная R в этом выражении имеет вполне конкретный физический смысл. Она показывает работу, которую выполнит 1 моль газа, если он будет расширяться при увеличении температуры на 1 кельвин (R = 8,314 Дж/(моль*К)).
Другие формы записи универсального уравнения
Помимо записанной выше формы универсального уравнения состояния для газа идеального, существует уравнения состояния, которые используют другие величины. Приведем их ниже:
- P * V = m / M * R * T;
- P * V = N * kB * T;
- P = ρ * R * T / M.
В этих равенствах m - масса газа идеального, N - число частиц в системе, ρ - плотность газа, M - значение молярной массы.
Напомним, что записанные выше формулы справедливы только в случае использования единиц системы СИ для всех физических величин.
Пример задачи
Получив необходимые теоретические сведения, решим следующую задачу. Чистый азот находится при давлении 1,5 атм. в баллоне, объем которого составляет 70 литров. Необходимо определить количество молей идеального газа и его массу, если известно, что он находится при температуре 50 °C.
Для начала запишем все единицы измерения в СИ:
1) P = 1,5 * 101325 = 151987,5 Па;
2) V = 70 * 10-3 = 0,07 м3;
3) T = 50 + 273,15 = 323,15 К.
Подставим теперь эти данные в уравнение Клапейрона-Менделеева, получим значение количества вещества:
- n = P * V / (R * T) = 151987,5 * 0,07 / (8,314 * 323,15) = 3,96 моль.
Для определения массы азота следует вспомнить его химическую формулу и посмотреть значение молярной массы в таблице Менделеева для этого элемента:
- M(N2) = 14 * 2 = 0,028 кг/моль.
Масса газа будет равна:
- m = n * M = 3,96 * 0,028 = 0,111 кг.
Таким образом, количество азота в баллоне равно 3,96 моль, его масса составляет 111 грамм.

