Учителя начальных классов хорошо знают, что умножение и деление многозначных чисел в 4 классе дается детям трудно, поскольку изучаются азы математических алгоритмов высшего порядка. Старые методики признаны неэффективными в обучении. Вызвано это тем, что класс редко обращает внимание на сухие факты, предпочитая справляться помощью калькулятора. Описанная ниже методология поможет зажечь интерес в детях, отвлекая от сложной последовательности действий по частям.
Советы по преподаванию
 Вам будет интересно:Унция - это... Сколько в унции грамм? Жидкая унция
Вам будет интересно:Унция - это... Сколько в унции грамм? Жидкая унция
Взрослые люди, которым процесс вычисления кажется элементарным, не всегда понимают, что для ребенка это новая информация. Проявите терпение и воспользуйтесь рекомендациями для сохранения дружелюбной обстановки во время изучения:
 Вам будет интересно:Добротность динамика: формула расчета, как снизить или повысить добротность динамика
Вам будет интересно:Добротность динамика: формула расчета, как снизить или повысить добротность динамика
 Вам будет интересно:Дискурсивный анализ: понятие и роль в современной лингвистике
Вам будет интересно:Дискурсивный анализ: понятие и роль в современной лингвистике
Не забывайте мотивировать детей, проводить интерактивные игры или подбадривать, чтобы вселить уверенность в действиях. Поддержка является ключом ко всему.
Математическая терминология
Прежде чем перейти к делению многозначного числа на однозначное, необходимо выучить несколько несложных правил и терминов:
- Каждое число, кроме нуля, является либо отрицательным, либо положительным. Если знак не отображается, то мы автоматически приписываем впереди плюс.
- Каждая цифра в задаче обозначается своим определением. Например, 6/2=3 – первое является делимым. Это означает, что число разбивается на части при применении математических азов. Далее, 2 – делитель, а 3 – произведение.
- Если вы проходите дроби, то акцентируйте внимание, что это не одно и то же, поскольку здесь присутствуют числитель и знаменатель.
Некоторые другие правила:
Но для того чтобы освоить деление многозначного числа на однозначное в 4 классе, недостаточно лишь знать свод правил и перейти к закреплению материала, необходимо повторить противоположную систему функции.
Принцип умножения двух чисел
Знание азов спасает от дальнейших проблем с алгеброй. Именно поэтому следует уделить внимание предыдущим урокам. В математике деление многозначных чисел происходит на основе изучения таблицы умножения.
 Вам будет интересно:Повышение квалификации государственных служащих: профессиональная переподготовка, обзор учреждений
Вам будет интересно:Повышение квалификации государственных служащих: профессиональная переподготовка, обзор учреждений
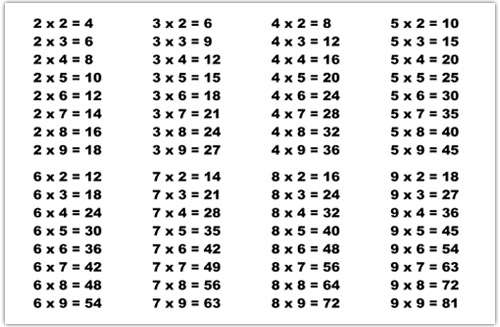
Так, структурированная табличка подскажет ответ при основных операциях с любой цифрой. Она пригодится не только в начальной школе, но и при столкновении с высшей математикой. Иначе говоря, ее необходимо закрепить на сознательном уровне ребенка так, чтобы она стала таким же естественным процессом, как есть и спать.
Итак, если попросить учеников умножить 3×5, то они с легкостью могут разложить пример на сложение трех пятерок. Вместо того чтобы в дальнейшем мучиться с большими числами, достаточно запомнить показатели таблички.
Самый простой метод умножения – визуализация цифр в предметы. Предположим, что нам нужно узнать ответ в случае 4×3. Первое число можно представить в виде игрушечных машинок, а 3 - как количество групп, которые мы хотим добавить в коллекцию.
Частая практика в умножении в будущем значительно облегчает процесс деления многозначных чисел. Довольно скоро основы сами закрепятся, если проявлять упорство и регулярно повторять материал. Рекомендуется создать строчную диаграмму с 1 до 12, как показано на рисунке:
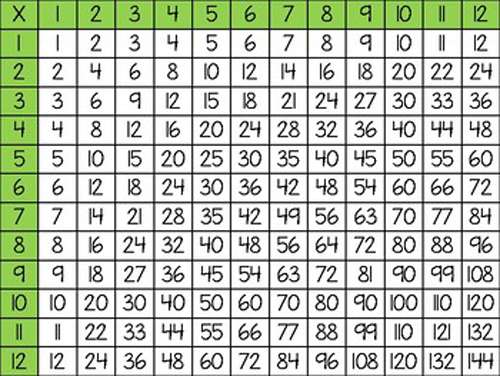
Пользоваться ею достаточно просто: проведите пальцем по строке от необходимой цифры к значению другой. Диаграмму также можно включить в ежедневные занятия. Благодаря ей ребенок сможет быстро сориентироваться и быстрее закрепить материал.
Первый шаг: как преподнести
Теперь, когда вы приступили к методам деления многозначного числа на однозначное, вы должны четко обозначить математическую операцию. Дело в том, что дети склонны к элементарным ошибкам в связи с тем, что материал является для них новым. Нередко они могут делить на ноль или путать плюс с минусом. Проявите терпение, ведь и вы не сразу начинали с дифференциалов. Объясните, что предметы разделяются на несколько групп одного и того же числа.
После того как простое понимание будет закреплено, приступайте к постепенному знакомству с рабочими таблицами. Акцентируйте внимание на важности противоположных функциях. Деление и умножения тесно связаны между собой, потому решения примеров высшей математики невозможны без задействования двух вычислительных техник. Чередуйте цифры в логичной последовательности, меняйте их местами:
5×3 = 15, 3×5 = 15, 15/3 = 5, 15/5 = 3.
Когда ребенок пройдет теоретический урок деления многозначных чисел на число, то постигнет всю концепцию, проследив полноценную структуру. После этого и приступайте к практической части. Продемонстрируйте, какими знаками обозначаются примеры, выслушайте вопросы.
Начните с практики деления многозначных чисел на 1, 2 и 3, затем постепенно переходите к 9. Запаситесь черновиками для подробного разбора. Как только основная схема решения станет понятной, дети подключатся и к более тяжелым задачам.
Примеры с одинаковым знаком
Теперь, когда мы познакомились со всеми особенностями, важно рассмотреть первую проблему с делением чисел. Довольно часто дети путаются в знаках, расположенных перед цифрами. Как же представить 15/3? Оба числа являются положительными и будут давать соответствующий итог. Ответ: 5 или +5. Плюс ставить не обязательно, поскольку его не принято обозначать.
Но как же поступить, если примеры деления многозначных чисел стали с минусом? Достаточно обратить внимание на его расположение.
Так, -15/3 = 5 или +5.
Почему же знак оказался положительным? Дело в том, что каждая проблема деления может быть выражена в виде умножения. Отсюда следует, что 2×3 =6 записывается как деление 6/3 = 2. Правило чередования знака в системе умножения говорит нам, что 5×-3 = -15. Один из способов обозначить все это как проблему деления -15/-3 = 5, что аналогично -15/-3.
Таким образом, целесообразно выделить новое правило - частное двух отрицательных чисел является положительным.
Обратите внимание, что в обоих случаях единственное отличие от арифметической задачи состоит в том, что ребенок должен заранее предугадать знак, а уже после приступать к процессу вычисления. Данный способ эффективен и применяется повсеместно.
Еще одно важное правило – частное с двумя одинаковыми знаками всегда будет давать положительное значение. Используя эти знания, дети быстро освоятся в задачах.
Интерактивные игры
Для повышения скорости закрепления материала применяется деление многозначных чисел с карточками в 4 классе. Поговорите с ребенком и подчеркните, что при вычислении следует прибегать к обратной функции умножения.
Используйте карточки, предоставленные ниже, чтобы помочь детям запоминать и практиковать факты деления, или создайте собственные по похожему принципу.

Также обязательно проработайте значения на 6 и 9, которые даются детям с наибольшим трудом.
Рекомендации для создания карточек деления многозначных чисел:
Для достижения большего эффекта можно распечатать похожую стопку, но на проработку техники умножения.
Примеры с остатками
Дети, впервые познакомившиеся с делением, рано или поздно совершат ошибку или поделят случайное число так, что ответ покажется им неправильным. Остаток используется в более сложных примерах, когда невозможно обойтись без него. Порой произведение может состоять из 0 целых и длинных цифр за запятой. Важно объяснить ребенку, что подобное письменное деление многозначных чисел – нормально.

Некоторые задачи невозможно решить без сокращений, однако это уже совсем другая тема. Главное в данном случае - акцентировать внимание на том, что порой решение реально только с остатком.
Деление больших чисел: практика
 Вам будет интересно:Звездочет - это ученый, который изучает астрономию
Вам будет интересно:Звездочет - это ученый, который изучает астрономию
Современные дети довольно часто прибегают к математическим решениям с помощью техники. Когда они научатся правильно считать, им больше не понадобится волноваться о сложных функциях, тем более если в процессе жизнедеятельности регулярно повторять табличные значения и ловко использовать их. Суммы деления могут показаться пугающими. На самом же деле, как и практически все в математике, они будут логичны. Рассмотрим одну из задач деления многозначного числа на однозначное в 4 классе.
Представим, что автомобиль Толи нуждается в новых шинах. Все четыре ведущих колеса и одно запасное должны быть заменены. Водитель присмотрел выгодный вариант по замене стоимостью 480 руб., которая включала также примерку и утилизацию. Сколько будет стоить каждая шина?
Задача, которая стоит перед нами - вычислить, сколько составляет 480/5. Иначе говоря, это то же самое, что сказать, сколько 5 перейдет в 480.
Начинаем с деления 5 на 4 и сразу же сталкиваемся с проблемой, потому что первый показатель значительно выше второго. Поскольку нас интересуют только целые числа, мы мысленно ставим ноль и дугой выделяем цифры, превышающие 5. На данный момент это 48.
Следующим шагом будет использование того числового значения, которое бы входило 5 раз в 48. Для ответа на этот вопрос обращаемся к таблице умножения и ищем цифру в столбике.
9×5 = 45 и 10×5 = 50.
Число находится между двумя приведенными значениями. Нас интересует 45, поскольку оно меньше 48 и его реально вычесть без минусового результата. Так, 5 входит в 45 9 раз, однако не совсем так, как хотелось, потому здесь формируется остаток - 3.
Записываем 9 в правый столбик и решаем 48-45 = 3. Следовательно, 5×9 = 45, +3, чтобы получить 48.
Опускаем ноль вниз, чтобы 3 превратилось в 30. Теперь надо разделить 30 на 5 или выяснить, сколько раз 5 переходит в 30. Благодаря табличным значениям легко обнаружить ответ - 6. Потому что 5×6 = 30. Это позволяет поделить без остатка. Более подробная техника решения рассмотрена на рисунке ниже.
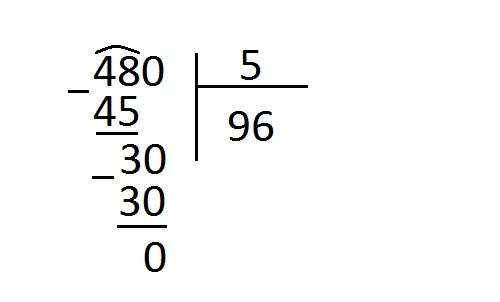
Поскольку делить больше нечего, мы получили в ответе 96. Проведем проверку обратным действием.
480/5 = 96 и 96×5 = 480
Каждая новая шина обойдется Толе в 96 рублей.
Как научить делению: советы для родителей
Дети 9-11 лет связывают математические факты в несколько раз быстрее. Например, они понимают, что умножение и деление многозначных чисел тесно пересекается между собой, как 36/4 и 18×2 имеет одинаковую структурность исчисления.

Ребенку не составит труда определить целостность решения, перечислить кратные и объяснить формирование остатка. Однако автоматизация требует времени, потому предоставляем вам обучающие игры, чтобы помочь закрепить материал:
Заключение
Разобрав основы математических операций, дети перестанут волноваться, что у них ничего не получается. Азы закладываются в нас с детства, потому не поленитесь уделить внимание счету и делению, поскольку в будущем алгебра будет лишь сложнее и овладеть некоторыми уравнениями без углубленных знаний, станет невозможно.
