Призма - это одна из объемных фигур, свойства которой изучают в школе в курсе пространственной геометрии. В данной статье рассмотрим конкретную призму - шестиугольную. Что это за фигура, как найти объем правильной шестиугольной призмы и площадь ее поверхности? Ответы на эти вопросы содержатся в статье.
Фигура призма
Предположим, что мы имеем произвольный многоугольник с числом сторон n, который находится в некоторой плоскости. К каждой вершине этого многоугольника построим вектор, который не будет лежать в плоскости многоугольника. С помощью этой операции мы получим n одинаковых векторов, вершины которых образуют многоугольник, в точности равный исходному. Фигура, ограниченная двумя одинаковыми многоугольниками и параллельными линиями, соединяющими их вершины, называется призмой.
 Вам будет интересно:Одушевленные и неодушевленные существительные - как определить? Одушевленные и неодушевленные существительные
Вам будет интересно:Одушевленные и неодушевленные существительные - как определить? Одушевленные и неодушевленные существительные
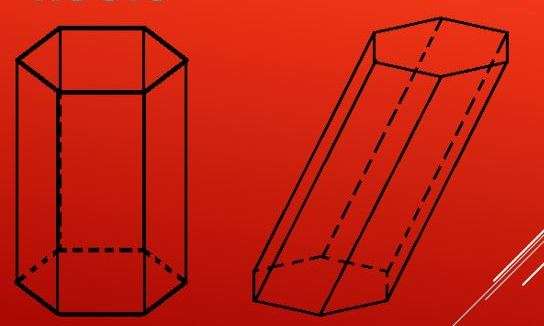
Гранями призмы являются два основания, представленные многоугольниками с n сторонами, и боковые n поверхностей-параллелограммов. Количество ребер Р фигуры связано с числом ее вершин В и граней Г формулой Эйлера:
 Вам будет интересно:Значение слова «подвизаться» в быту и в храме
Вам будет интересно:Значение слова «подвизаться» в быту и в храме
Р = В + Г - 2
Для многоугольника с n сторонами получаем n + 2 грани и 2 * n вершин. Тогда количество ребер будет равно:
Р = В + Г - 2 = 2 * n + n + 2 - 2 = 3 * n
Самой простой призмой является треугольная, то есть основанием у нее является треугольник.
Классификация призм достаточно разнообразна. Так, они могут быть правильными и неправильными, прямоугольными и косоугольными, выпуклыми и вогнутыми.
Шестиугольная призма
Эта статья посвящена вопросу объема правильной шестиугольной призмы. Сначала познакомимся ближе с этой фигурой.
Как следует из названия, основание шестиугольной призмы является многоугольником с шестью сторонами и шестью углами. В общем случае таких многоугольников можно составить великое множество, однако для практики и для решения геометрических задач важен один единственный случай - правильный шестиугольник. У него все стороны равны между собой, а каждый из 6 углов составляет 120 o. Построить этот многоугольник можно легко, если разделить окружность на 6 равных частей тремя диаметрами (они должны пересекаться под углами 60 o).
Правильная шестиугольная призма предполагает не только наличие правильного многоугольника в ее основании, но и тот факт, что все боковые стороны фигуры должны являться прямоугольниками. Это возможно только в случае, если боковые грани будут перпендикулярны шестиугольным основаниям.
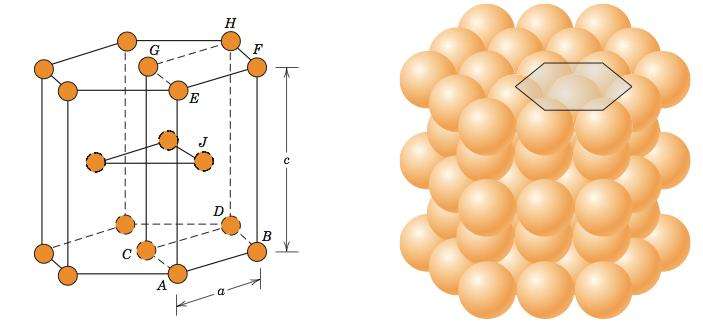
Правильная шестиугольная призма - это достаточно совершенная фигура, которая встречается в быту и природе. Стоит только вспомнить о форме пчелиных сот или о шестигранном гаечном ключе. В области нанотехнологий также часто встречаются шестиугольные призмы. Например, кристаллические решетки ГПУ и C32, которые реализуются при определенных условиях в титане и цирконии, а также решетка графита имеют форму шестиугольных призм.
Площадь поверхности шестиугольной призмы
Перейдем теперь непосредственно к вопросу вычисления площади и объема призмы. Сначала рассчитаем площадь поверхности этой фигуры.
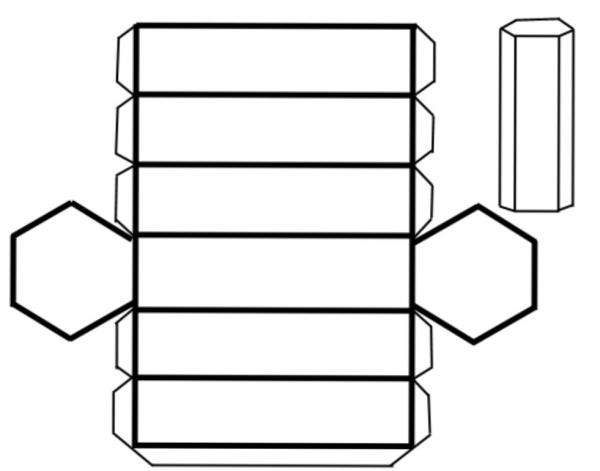
Площадь поверхности любой призмы вычисляется с помощью следующего равенства:
S = 2 * So + Sb
То есть искомая площадь S равна сумме площадей двух оснований So и площади боковой поверхности Sb. Для определения величины So можно поступить двумя способами:
- Вычислить ее самостоятельно. Для этого шестиугольник разбивается на 6 равносторонних треугольников. Зная, что площадь одного треугольника равна половине произведения высоты на основание (длину стороны шестиугольника), можно найти площадь рассматриваемого многоугольника.
- Воспользоваться известной формулой. Она приведена ниже:
Sn = n / 4 * a2 * ctg(pi / n)
Здесь a - длина стороны правильного многоугольника, имеющего n вершин.
Очевидно, что оба способа приводят к одному результату. Для правильного шестиугольника площадь равна:
So = S6 = 3 * √3 * a2 / 2
Площадь боковой поверхности найти просто, для этого следует умножить основание каждого прямоугольника a на высоту призмы h, полученное значение умножить на число таких прямоугольников, то есть на 6. В итоге:
Sb = 6 * a * h
Пользуясь формулой для полной площади поверхности, для правильной шестиугольной призмы получаем:
S = 3 * √3 * a2 + 6 * a * h = 3 * a * (√3 * a + 2 * h)
Как найти объем призмы?
Объем - это физическая величина, которая отражает область пространства, занимаемую объектом. Для призмы рассчитать эту величину можно по следующей формуле:
V = So * h
Это выражение дает ответ на вопрос о том, как найти объем призмы произвольной формы, то есть необходимо площадь основания So умножить на высоту фигуры h (расстояние между основаниями).
Заметим, что приведенное выражение справедливо для любой призмы, включая вогнутые и косоугольные фигуры, образованные неправильными многоугольниками в основании.
Формула объема призмы шестиугольной правильной
На данный момент мы рассмотрели все необходимые теоретические выкладки, чтобы получить выражение для объема рассматриваемой призмы. Для этого достаточно площадь основания умножить на длину бокового ребра, которая является высотой фигуры. В итоге формула объема шестиугольной призмы примет вид:
V = 3 * √3 * a2 * h / 2
Таким образом, расчет объема рассматриваемой призмы предполагает знание всего двух величин: длины стороны ее основания и высоты. Эти две величины однозначно определяют объем фигуры.
Сравнение объемов шестиугольной призмы и цилиндра

Выше было сказано, что основание шестиугольной призмы может быть легко построено с использованием окружности. Также известно, что если увеличивать число сторон правильного многоугольника, то его форма будет приближаться к окружности. В связи с этим представляет интерес рассчитать, на сколько объем правильной шестиугольной призмы отличается от этого значения для цилиндра.
Для ответа на поставленный вопрос необходимо вычислить длину стороны шестиугольника, вписанного в окружность. Можно легко показать, что она равна радиусу. Обозначим радиус окружности буквой R. Предположим, что высота цилиндра и призмы равна некоторому значению h. Тогда объем призмы равен следующему значению:
Vp = 3 * √3 * R2 * h / 2
Объем цилиндра определяется по той же формуле, что и объем для произвольной призмы. Учитывая, что площадь круга равна pi * R2, для объема цилиндра имеем:
Vс = pi * R2 * h
Найдем отношение объемов этих фигур:
Vp / Vс = 3 * √3 * R2 * h / 2 / (pi * R2 * h) = 3 * √3 / (2 * pi)
Число "пи" равно 3,1416. Подставляя его, получаем:
Vp / Vс = 0,827
Таким образом, объем правильной шестиугольной призмы составляет около 83 % от объема цилиндра, в который она вписана.

