Нахождение площади трапеции является одним из основных действий, которое позволяет решать множество задач геометрии. Также в КИМ по математике ОГЭ и ЕГЭ есть множество задач, для решения которых необходимо знать, как искать площадь этой геометрической фигуры. В данной статье будут рассмотрены все формулы площади трапеции.
Что собой представляет данная фигура?

Прежде чем рассматривать все формулы площади трапеции, необходимо знать, что это такое, потому что без четкого определения невозможно грамотно пользоваться формулами и свойствами данной фигуры. Трапеция - четырехугольник, две стороны которого расположены напротив друг друга, и если продолжить их до бесконечных прямых, то они никогда не пересекутся (данные стороны являются основаниями фигуры). Две другие стороны могут обладать тупыми и острыми углами и называются боковыми (при этом, если боковые стороны ее одинаковы, а углы при основании попарно равны друг другу, то такая трапеция называется равнобокой). Все формулы площади этого четырехугольника рассмотрены далее.
Все формулы площади трапеции
 Вам будет интересно:Объем треугольной призмы: формула общего типа и формула для правильной призмы
Вам будет интересно:Объем треугольной призмы: формула общего типа и формула для правильной призмы
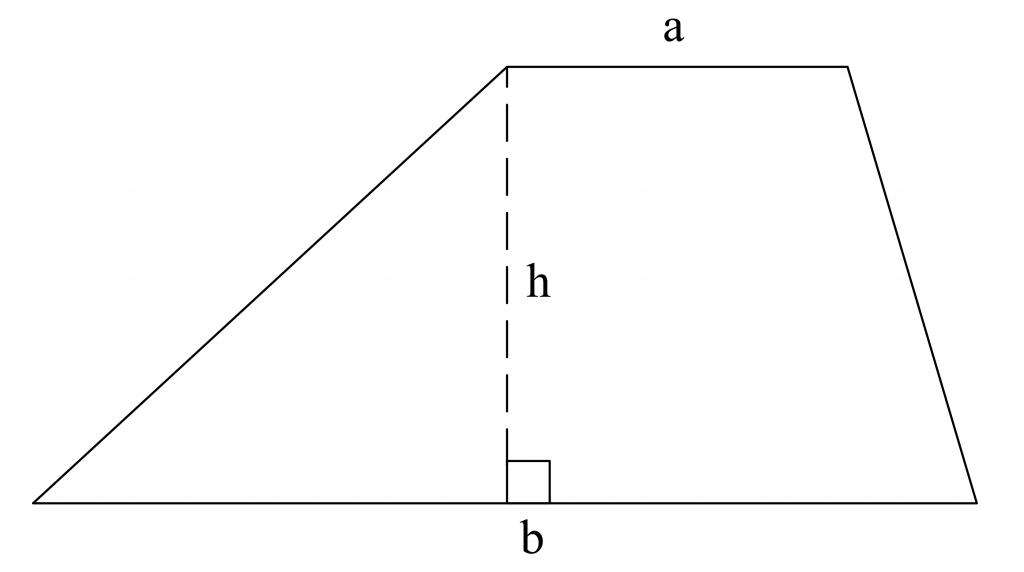
В геометрии существует множество формул нахождения площадей фигур, что является как плюсом, так и минусом. Как же найти площадь трапеции?
Свойства биссектрисы трапеции
Как и биссектриса равнобедренного треугольника, проведенная к основанию, прямая, делящая угол пополам, данной фигуры обладает своими свойствами, которые пригодятся при решении задач по геометрии.
Заключение
В данной статье были предложены все формулы площади трапеции. Большинство из них не рассматривается в учебниках геометрии, но при этом все они необходимы для успешного решения задач.
