В школьном курсе геометрии изучаются свойства различных видов призм, включая шестиугольную. Последняя часто встречается при рассмотрении кристаллических решеток металлов, поэтому знание ее характеристик важно при определении свойств этого класса материалов. Данная статья посвящена вопросу площади основания правильной шестиугольной призмы.
Объемная фигура - призма
В геометрии под призмой понимают такую фигуру, которая образована двумя одинаковыми многоугольниками, расположенными параллельно друг другу, и некоторым числом параллелограммов, соединяющих вершины названных многоугольников. Если основание образовано многоугольником с n вершинами, то количество параллелограммов также будет равно n.
Вам будет интересно:Жить - это не только существовать
Призмы характеризуются по типу многоугольника в основании (правильные и неправильные треугольные, четырехугольные и так далее), который может быть вогнутым и выпуклым, и по углу между боковыми гранями (параллелограммами) и основанием (прямоугольные и косоугольные).
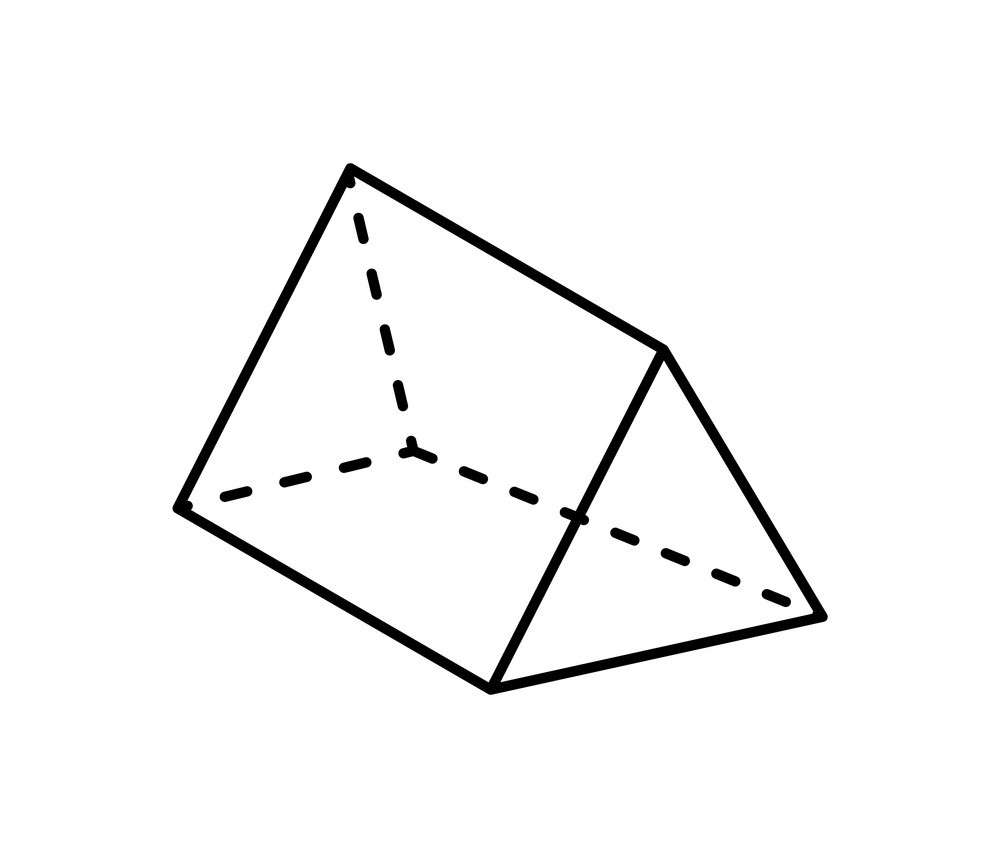
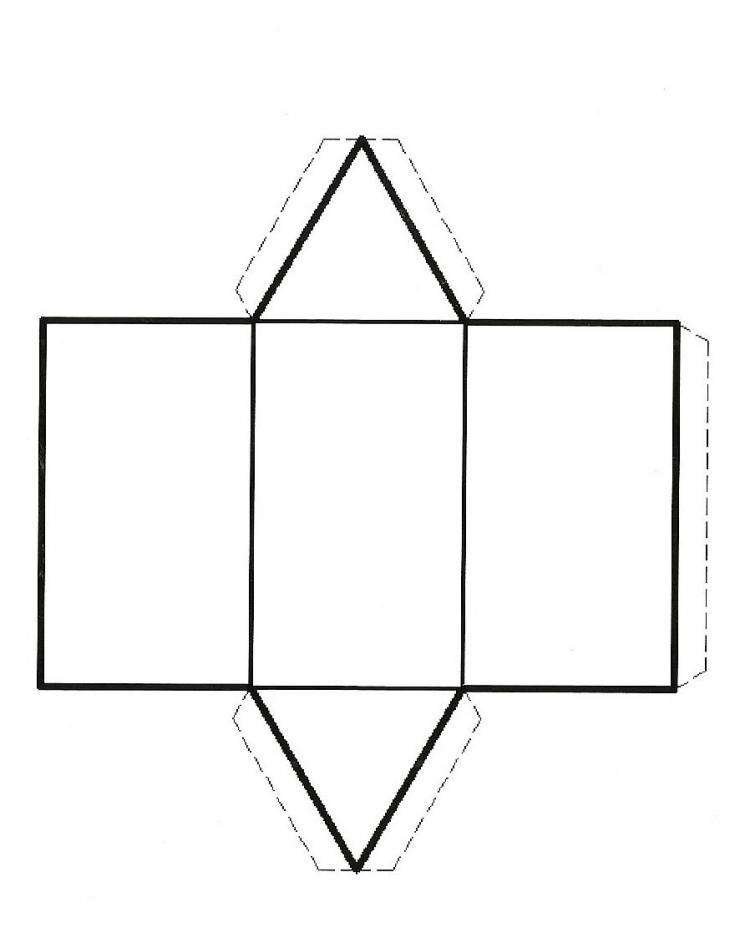
Основными элементами любой призмы являются ее грани (Г), ребра (Р) и вершины (В). На рисунке выше приведена для примера треугольная призма. Как видно, она имеет 6 вершин (по 3 для каждого основания). Ниже приведена развертка этой призмы. Рисунок показывает, что она состоит из 5 граней: 2 треугольника и 3 прямоугольника.
Вам будет интересно:Северо-Кавказский федеральный университет - источник качественного образования
Чтобы посчитать число ребер рассматриваемой фигуры, следует применить теорему Эйлера:
Р = В + Г - 2
Это выражение дает число ребер для этой призмы, равное 9. Действительно, если обратиться к трехмерному изображению призмы выше, то можно увидеть, что 6 ребер образуют основания фигуры, и еще 3 ребра являются результатом пересечения прямоугольников.
Призма шестиугольная
Перед рассмотрением вопроса площади основания правильной шестиугольной призмы, сначала познакомимся с этой фигурой. Из названия и приведенной выше классификации призм понятно, что речь пойдет о фигуре, в основании которой лежит шестиугольник. Это означает, что число сторон в такой призме будет равно 8 (два основания и шесть параллелограммов), а число вершин составит 12 (6 + 6). Тогда количество ребер будет равно:
Р = 12 + 8 - 2 = 18
Из этих 18-ти ребер основаниям принадлежат 12.
Если в основании находится правильный шестиугольник, а углы между боковыми сторонами (параллелограммами) и основаниями равны 90o, то такая фигура будет называться прямоугольной призмой с правильным шестиугольником в основании, или просто правильной шестиугольной призмой. Ее схематическое изображение приводится ниже.
В правильной шестиугольной призме все ребра равны только в том случае, если c = a, где c - высота (длина бокового ребра) и a - длина стороны шестиугольника. В общем случае c ≠ a.
Далее приведем формулы для расчета площади поверхности и объема рассматриваемой призмы. Чтобы это сделать, необходимо знать площадь основания правильной шестиугольной призмы.
Площадь шестиугольника
Получим формулу площади правильного шестиугольника. Для этого рассмотрим эту плоскую фигуру, которая изображена на рисунке ниже.
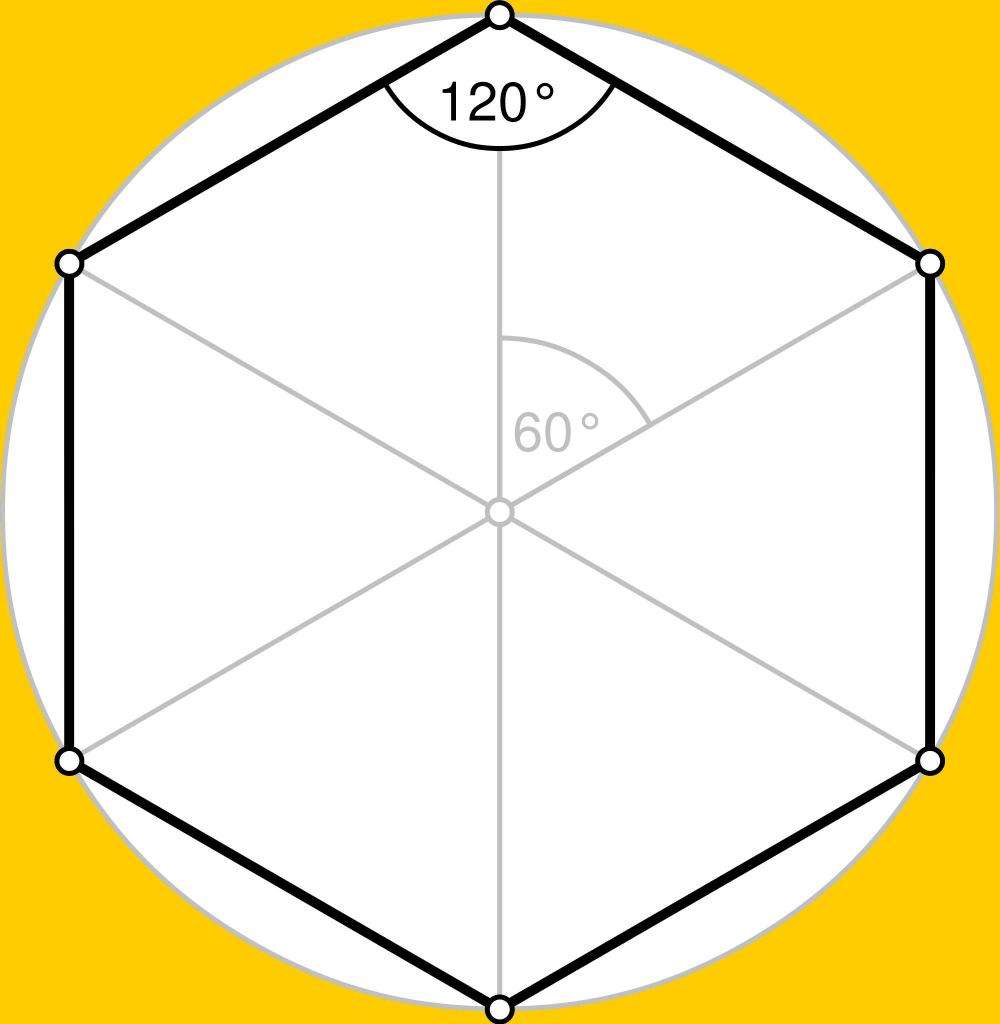
Видно, что многоугольник состоит из шести одинаковых сторон, которые образуют угол 120o. Поскольку этих углов шесть, то их сумма составит 720o.
Рисунок также показывает, что правильный шестиугольник гармонично вписывается в окружность. Если соединить центр окружности с каждой вершиной фигуры, то получим 6 одинаковых треугольников. Поскольку угловая мера всей окружности составляет 360o, то соответствующие углы треугольника равны 60o (360o/6). Они обозначены на рисунке. Поскольку каждый серый отрезок делит угол шестиугольника пополам, то оставшиеся два треугольника также равны по 60o. Это означает, что изображенные 6 треугольников являются равносторонними. Длина каждой из их сторон равна стороне шестиугольника, обозначим ее буквой a.
Из курса геометрии известно, что площадь S3 любого треугольника равна произведению его высоты h на сторону a, к которой она проведена, деленному пополам, то есть:
S3 = h*a/2
Длину h легко вычислить, используя понятие о тригонометрической функции. Она равна:
h = a*cos(30o) = a*√3/2
Тогда площадь всего треугольника равна:
S3 = √3*a2/4
Умножая эту площадь на 6, получаем формулу площади правильного шестиугольника:
S6 = 6*S3 = 3*√3*a2/2
Для полноты информации следует отметить, что существует формула площади правильного многоугольника с произвольным количеством сторон n. Ниже приведено соответствующее выражение:
Sn = n/4*a2*ctg(pi/n)
Если подставить в это выражение значение n = 6, то мы получим формулу площади основания правильной шестиугольной призмы, которая совпадет с приведенной выше.
Заметим, что деление шестиугольника на 6 равносторонних треугольников означает, что шестиугольная призма состоит из 6 правильных треугольных призм.
Площадь поверхности
Полная площадь поверхности любой призмы может быть получена, если сложить соответствующие площади So для двух оснований и для боковой поверхности Sb, представленной параллелограммами:
S = 2*So + Sb
Изучим развертку рассматриваемого вида призмы, которая приведена на рисунке ниже.
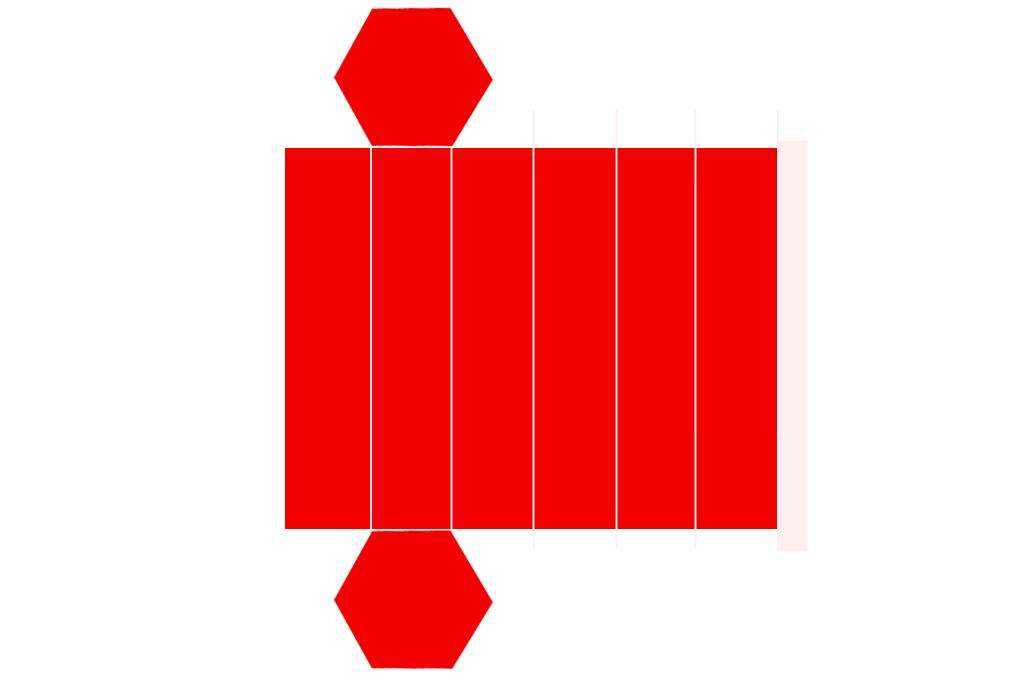
Мы видим, что призма состоит из двух одинаковых шестиугольников и 6 прямоугольников. Обозначим сторону основания буквой a, а стороны прямоугольников буквами a и c (сторона a является общей для шестиугольника и прямоугольника). В таком случае площадь полной поверхности шестиугольной призмы будет составлять:
S = 2*3*√3*a2/2 + 6*a*c = 3*a*(√3*a + 2*c)
Объем призмы
Эта важная величина для любого реального объекта в случае призмы находится просто: необходимо лишь умножить площадь основания на высоту фигуры, то есть:
V = So*h
Поскольку мы рассматриваем прямоугольную призму, то ее высота равна длине бокового ребра, то есть h = c. Тогда формула для объема правильной шестиугольной призмы запишется в виде:
V = 3*√3*a2*c/2
Таким образом, для определения площади и объема рассматриваемой фигуры необходимо знать длину ее ребра в основании и на боковой поверхности.
Для чего нужно знать свойства шестиугольной призмы?
Как было сказано во введении, эти призмы встречаются в природе в металлах. В частности, кристаллическая атомная упаковка титана, цинка, циркония, магния и некоторых других металлов имеет форму шестиугольной призмы, в основании которой лежат 7 атомов (6 в вершинах и 1 в центре). От соотношения длины ребра этой фигуры к длине стороны основания зависят многие механические свойства этих металлов (деформационные и упругие характеристики).
Выше приведен пример этой упаковки атомов, который носит сокращенное название ГПУ (гексагональная плотная упаковка).
