Плоскость является геометрическим объектом, свойства которого используют при построении проекций точек и линий, а также при вычислении расстояний и двугранных углов между элементами объемных фигур. Рассмотрим в данной статье, с помощью каких уравнений можно изучать расположение в пространстве плоскостей.
Определение плоскости
Каждый интуитивно представляет, о каком объекте пойдет речь. С геометрической точки зрения плоскость - это совокупность точек, любые вектора между которыми должны быть перпендикулярны некоторому одному вектору. Например, если имеется m разных точек в пространстве, то из них можно составить m*(m-1)/2 разных векторов, соединяя точки попарно. Если все вектора будут перпендикулярны некоторому одному направлению, тогда это является достаточным условием того, что все точки m принадлежат одной плоскости.
Общее уравнение
Вам будет интересно:Что значит "легок на помине" и какова история происхождения выражения?
В пространственной геометрии плоскость описывают с помощью уравнений, которые в общем случае содержат три неизвестные координаты, соответствующие осям x, y и z. Чтобы получить общее уравнение в координатах плоскости в пространстве, предположим, что имеется вектор n¯(A; B; C) и точка M(x0; y0; z0). Используя эти два объекта, можно однозначно определить плоскость.
Вам будет интересно:Врасплох – это испуг или всего лишь беспокойство?
Действительно, предположим, что имеется некоторая вторая точка P(x; y; z), координаты которой неизвестны. Согласно данному выше определению, вектор MP¯ должен быть перпендикулярен n¯, то есть произведение скалярное для них равно нулю. Тогда мы вправе записать следующее выражение:
(n¯*MP¯) = 0 или
A*(x-x0) + B*(y-y0) + C*(z-z0) = 0
Раскрывая скобки и вводя новый коэффициент D, получаем выражение:
A*x + B*y + C*z + D = 0, где D = -1*(A*x0 + B*y0 + C*z0)
Это выражение принято называть общим для плоскости уравнением. Важно запомнить, что коэффициенты, стоящие перед x, y и z, образуют координаты перпендикулярного к плоскости вектора n¯(A; B; C). Он совпадает с нормалью и является для плоскости направляющим. Для определения общего уравнения не имеет значения, куда направлен этот вектор. То есть построенные на векторах n¯ и -n¯ плоскости будут одинаковыми.
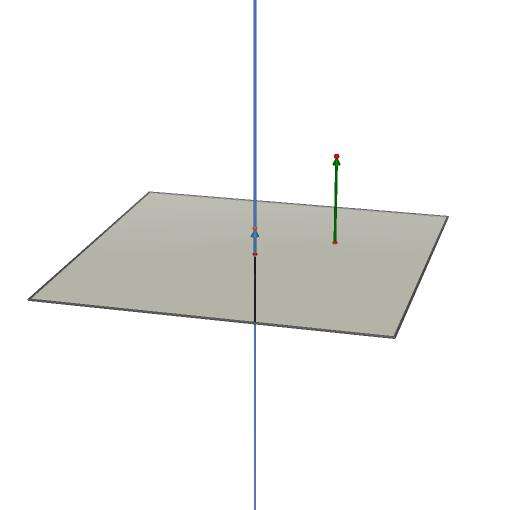
На рисунке выше показаны плоскость, нормальный к ней вектор и перпендикулярная прямая к плоскости.
Отсекаемые плоскостью отрезки на осях и соответствующее уравнение
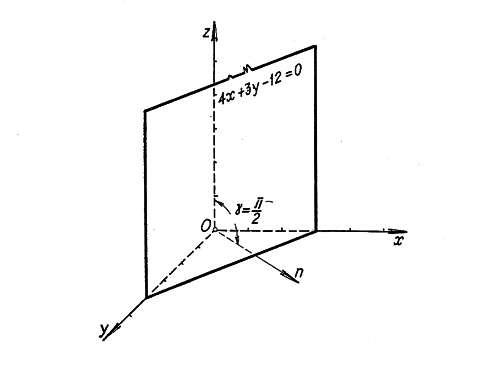
Общее уравнение позволяет с помощью простых математических операций определить, в каких точках плоскость будет пересекать координатные оси. Эту информацию важно знать, чтобы иметь представление о положении в пространстве плоскости, а также при изображении ее на чертежах.
Вам будет интересно:Гиалуроновая кислота: формула, состав, свойства, влияние на организм и применение
Для определения названных точек пересечения применяют уравнение в отрезках. Оно так называется по причине того, что явно содержит значения длин отрезков, отсекаемых плоскостью на осях координат, при ведении отсчета от точки (0; 0; 0). Получим это уравнение.
Запишем общее выражение для плоскости в следующем виде:
A*x + B*y + C*z = -D
Левую и правую части можно разделить на -D, не нарушая равенства. Имеем:
A/(-D)*x + B/(-D)*y + C/(-D)*z = 1 или
x/(-D/A) + y/(-D/B) + z/(-D/C) = 1
Обозначим знаменатели каждого члена новым символом, получаем:
p = -D/A; q = -D/B; r = -D/C тогда
x/p + y/q + z/r = 1
Это и есть упомянутое выше в отрезках уравнение. Из него следует, что значение знаменателя каждого члена указывает координату пересечения с соответствующей осью плоскости. Например, ось y она пересекает в точке (0; q; 0). Это легко понять, если подставить нулевые координаты x и z в уравнение.
Заметим, что если в уравнении в отрезках не будет присутствовать какой-либо переменной, то это означает, что соответствующую ось плоскость не пересекает. Например, дано выражение:
x/p + y/q = 1
Это означает, что плоскость отсечет отрезки p и q на осях x и y соответственно, а вот оси z она будет параллельна.
Вывод о поведении плоскости при отсутствии в ее уравнении некоторой переменной справедлив также для выражения общего типа, что демонстрирует рисунок ниже.
Уравнение параметрическое векторное
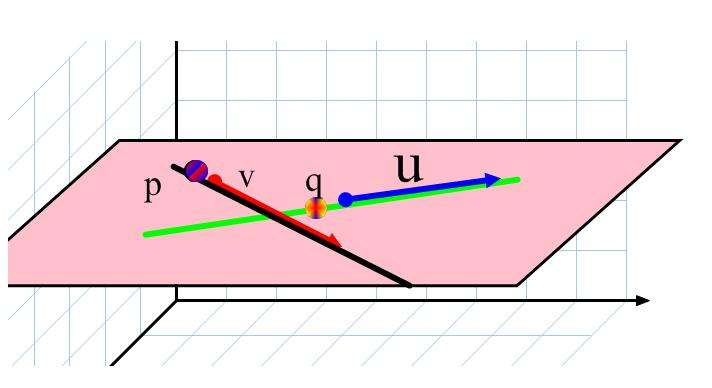
Существует третий вид уравнения, который позволяет описать в пространстве плоскости. Оно называется параметрическим векторным, поскольку задается двумя векторами, лежащими в плоскости, и двумя параметрами, которые могут принимать произвольные независимые значения. Покажем, как можно получить это уравнение.
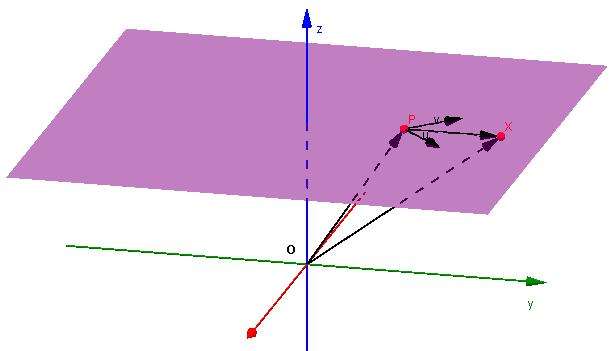
Предположим, что существует пара известных векторов u ¯(a1; b1; c1) и v¯(a2; b2; c2). Если они являются не параллельными, то с их помощью можно задать конкретную плоскость, если зафиксировать начало одного из этих векторов в известной точке M(x0; y0; z0). Если произвольный вектор MP¯ можно представить в виде комбинации линейной векторов u¯ и v¯, то это означает, что точка P(x; y; z) принадлежит той же плоскости, что и u¯, v¯. Таким образом, можно записать равенство:
MP¯ = α*u¯ + β*v¯
Или записывая это равенство через координаты, получим:
(x; y; z) = (x0; y0; z0) + α*(a1; b1; c1) + β*(a2; b2; c2)
Представленное равенство является уравнением параметрическим векторным для плоскости. В пространстве вектора на плоскости u¯ и v¯ называются образующими.
Далее при решении задачи будет показано, как это уравнение можно привести к общему виду для плоскости.
Угол между плоскостями в пространстве
Интуитивно понятно, что плоскости в трехмерном пространстве могут либо пересекаться, либо нет. В первом случае представляет интерес найти угол между ними. Расчет этого угла выполнить сложнее, чем угла между прямыми, поскольку речь идет о двугранном геометрическом объекте. Однако на помощь приходит уже упомянутый вектор направляющий для плоскости.
Геометрически установлено, что двугранный угол между двумя пересекающимися плоскостями точно равен углу между их векторами направляющими. Обозначим эти вектора как n1¯(a1; b1; c1) и n2¯(a2; b2; c2). Косинус угла между ними определяется из скалярного произведения. То есть сам угол в пространстве между плоскостями можно рассчитать по формуле:
φ = arccos(|(n1¯*n2¯)|/(|n1¯|*|n2¯|))
Здесь модуль в знаменателе используется, чтобы отбросить значение тупого угла (между пересекающимися плоскостями он всегда меньше или равен 90o).
В координатной форме это выражение можно переписать следующим образом:
φ = arccos(|a1*a2 + b1*b2 + c1*c2|/(√(a12 + b12 + c12)*√(a22 + b22 + c22)))
Плоскости перпендикулярные и параллельные
Если плоскости пересекаются, и образованный ими двугранный угол равен 90o, то они будут перпендикулярными. Примером таких плоскостей можно назвать прямоугольную призму или куб. Эти фигуры образованы шестью плоскостями. В каждой вершине названных фигур встречаются три плоскости, перпендикулярные друг другу.
Чтобы выяснить, являются ли рассматриваемые плоскости перпендикулярными, достаточно рассчитать скалярное произведение их нормальных векторов. Достаточным условием перпендикулярности в пространстве плоскостей является нулевое значение этого произведения.
Параллельными называются непересекающиеся плоскости. Иногда также говорят, что параллельные плоскости пересекаются в бесконечности. Условие параллельности в пространстве плоскостей совпадает с таковым условием для направляющих векторов n1¯ и n2¯. Проверить его можно двумя способами:
На рисунке показаны две параллельных плоскости.
Теперь приведем примеры решения двух интересных задач, используя полученные математические знания.
Как из векторного уравнения получить общий вид?
Речь идет о параметрическом векторном выражении для плоскости. Чтобы легче было понять ход операций и используемые математические приемы, рассмотрим конкретный пример:
(x; y; z) = (1; 2; 0) + α*(2; -1; 1 ) + β*(0; 1; 3 )
Раскроем это выражения и выразим неизвестные параметры:
x = 1 + 2*α;
y = 2 - α + β;
z = α + 3*β
Тогда:
α = (x - 1)/2;
β = y - 2 + (x - 1)/2;
z = (x - 1)/2 + 3*(y - 2 + (x - 1)/2)
Раскрывая скобки в последнем выражении, получаем:
z = 2*x-2 + 3*y - 6 или
2*x + 3*y - z - 8 = 0
Мы получили общий вид уравнения для плоскости, заданной в условии задачи в векторной форме
Как построить плоскость через три точки?
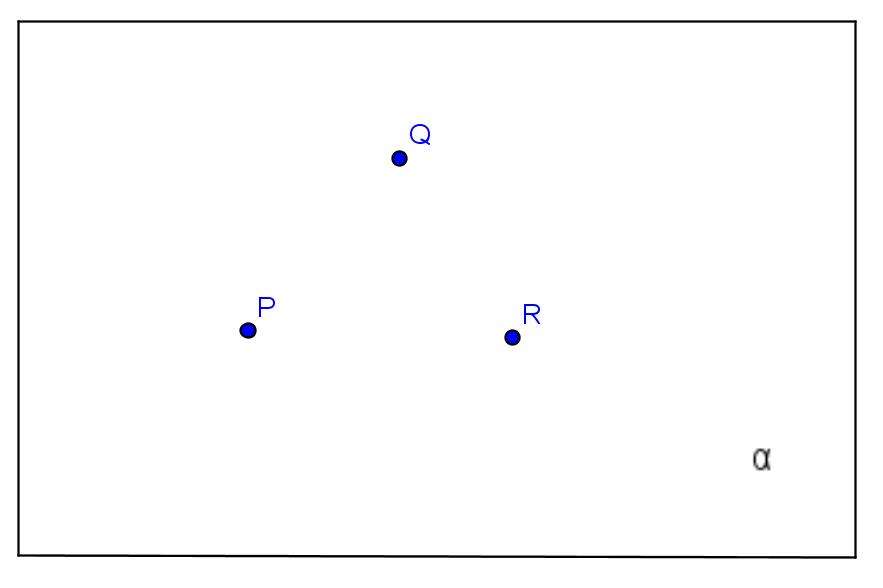
Провести через три точки единственную плоскость возможно, если эти точки не принадлежат некоторой одной прямой. Алгоритм решения этой задачи заключается в следующей последовательности действий:
- найти координаты двух векторов, соединив попарно известные точки;
- вычислить их векторное произведение и получить нормальный к плоскости вектор;
- написать общее уравнение, используя найденный вектор и любую из трех точек.
Приведем конкретный пример. Даны точки:
R(1; 2; 0), P(0; -3; 4), Q(1; -2; 2)
Координаты двух векторов равны:
RP¯(-1; -5; 4), PQ¯(1; 1; -2)
Их векторное произведение будет равно:
n¯ = [RP¯*PQ¯] = (6; 2; 4)
Взяв координаты точки R, получаем искомое уравнение:
6*x + 2*y + 4*z -10 = 0 или
3*x + y + 2*z -5 = 0
Рекомендуется проверять правильность результата путем подстановки координат оставшихся двух точек в это выражение:
для P: 3*0 + (-3) + 2*4 -5 = 0;
для Q: 3*1 + (-2) + 2*2 -5 = 0
Отметим, что можно было не находить векторное произведение, а сразу записать для плоскости уравнение в параметрическом векторном виде.