Конус является объемной фигурой вращения, которая часто появляется в геометрических задачах. Как и всякая фигура, он обладает рядом линейных характеристик, площадью поверхности и объемом. В данной статье рассмотрим, что представляет собой конус, а также приведем формулу образующей конуса.
Конус в геометрии

Многие ели в жаркий летний день мороженое-рожок. Вафельный стаканчик этого мороженого имеет форму конуса. В геометрии более строгое определение этой фигуры следующее: конус представляет собой поверхность, которая получается в результате соединения с помощью прямых отрезков всех точек некоторой плоской кривой с фиксированной точкой пространства, не лежащей в плоскости упомянутой кривой. Если кривая является эллипсом, то конус будет эллиптическим, если окружностью - то круглым и так далее.
 Вам будет интересно:Под сенью муз: художественная школа Мурманска
Вам будет интересно:Под сенью муз: художественная школа Мурманска
Данное выше геометрическое определение соответствует фигуре на рисунке ниже.
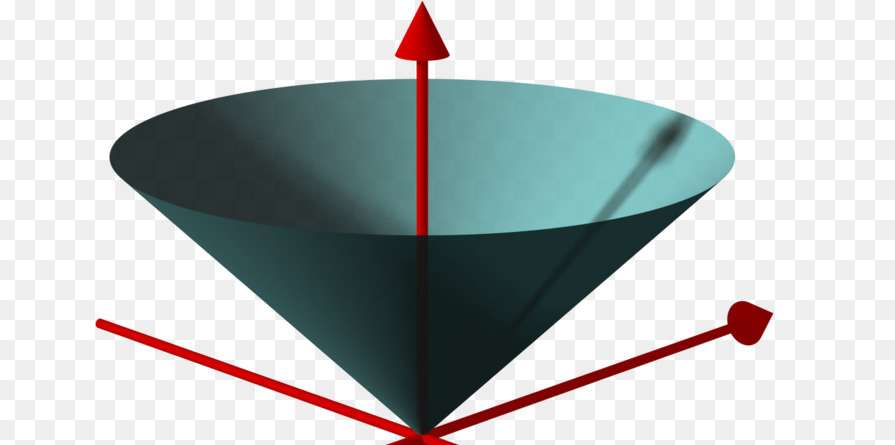
Здесь кривой, на которую опирается коническая поверхность, является окружность, центр которой лежит на вертикальной оси. Как видно из рисунка, хотя фигура является пространственной, но ее объем равен нулю. Если вместо окружности взять круг, тогда ограниченный этим кругом и конической поверхностью объем пространства будет объемом конуса.
Элементы фигуры
Перед тем как привести формулу образующей конуса, следует пояснить, из каких элементов состоит рассматриваемая пространственная фигура, и какие геометрические понятия используются для ее описания.
Ориентируясь на предыдущий рисунок, можно сказать, что конус образован двумя поверхностями:
- конической, которая называется также боковой;
- плоской фигурой (круг на рисунке), которая называется основанием конуса.
В отличие от полиэдров, конус не имеет граней и ребер, однако у него имеется одна единственная вершина, которая сверху ограничивает коническую поверхность. На предыдущем рисунке вершина находится в начале координат.
Для рассматриваемой фигуры также используют понятия образующей и направляющей. Что такое образующая конуса, и что такое его направляющая. Начнем с определения последней. Направляющей является кривая, ограничивающая основание фигуры. Названа она так, поскольку вдоль нее движется образующая, описывая коническую поверхность. Направляющая часто называется директрисой.
Образующая - это прямой отрезок, который соединяет вершину фигуры и любую точку направляющей. Образующих у конуса бесконечное множество. Их совокупность определяет коническую поверхность. Образующую также называют генератрисой.
Круглый прямой конус
Как отмечалось выше, основание конуса может быть ограничено любой плоской кривой. Тем не менее на практике и в геометрических задачах часто встречается круглый конус. Его и будем рассматривать далее в статье.
Круглый конус может быть прямым или наклонным. В первом случае перпендикуляр, проведенный из его вершины к основанию, пересекает последнее в центре круга. Прямой круглый конус является симметричной фигурой вращения, которую можно получить с помощью прямоугольного треугольника. Рисунок ниже показывает, как это делается.
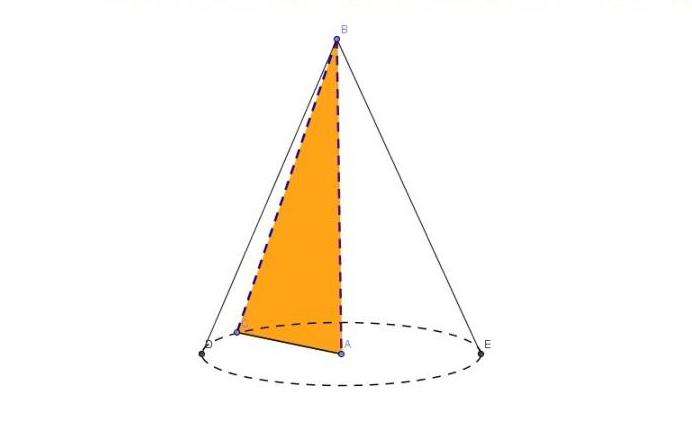
На рисунке показан прямоугольный треугольник, который стоит на одном из своих катетов. Вокруг другого катета, являющегося осью, происходит вращение плоской фигуры. Во время вращения гипотенуза треугольника описывает коническую поверхность.
Линейные характеристики круглого прямого конуса
Ниже показан чертеж круглого конуса, на котором введены обозначения. Величина h - это высота фигуры, r - круглого основания радиус, который называется радиусом конуса, s - длина образующей.
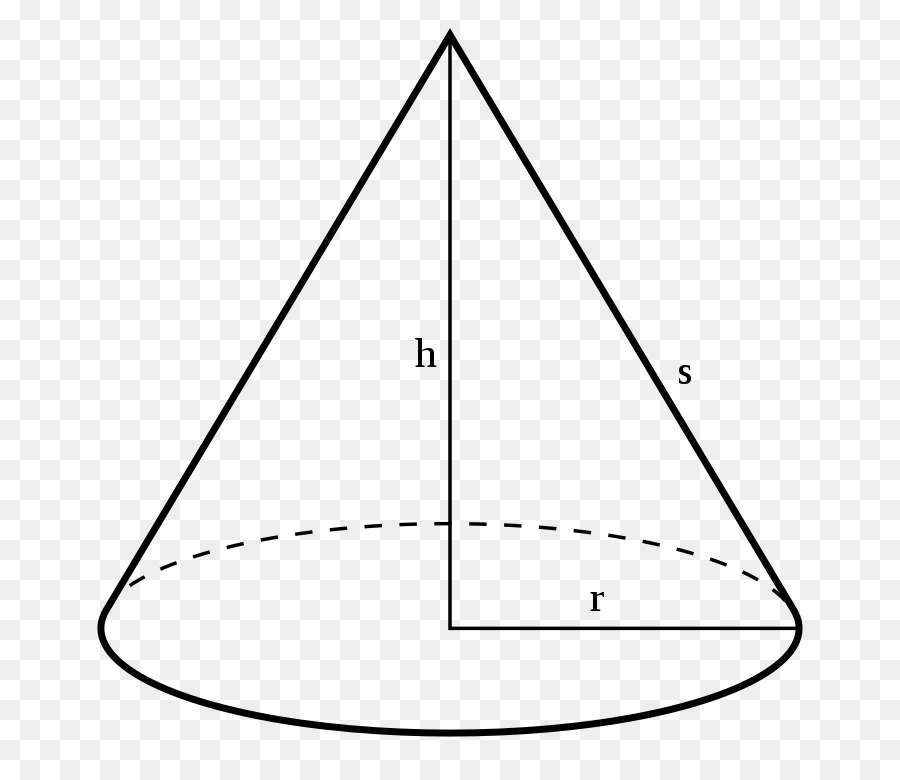
Очевидно, что все образующие s рассматриваемой фигуры имеют одинаковую длину. Это важное свойство присуще только прямому круглому конусу. Угол между любой образующей и осью вращения конуса является постоянной величиной при известных значениях r и h.
Как видим из рисунка, стороны r, h и s ограничивают прямоугольный треугольник. Этот факт позволяет применить теорему Пифагора для записи математического равенства, связывающего названные линейные характеристики конуса. Равенство имеет форму:
s2 = r2 + h2
Это равенство содержит ответ на вопрос о том, как найти длину образующей конуса. Если известны радиус фигуры и ее высота, тогда:
s = √(r2 + h2)
Далее, на примерах решения задач покажем, как пользоваться формулой образующей конуса.
Задача с площадью конической поверхности и длиной окружности основания
Дан прямой конус с круглым основанием. Известно, что площадь его боковой поверхности равна 120 см2, а длина окружности основания составляет 30 см. Чему равна образующая конуса?
Решение этой задачи предполагает использование двух дополнительных формул, которые не были рассмотрены в статье. Приведем их ниже:
Sb = pi × r × s;
L = 2 × pi × r
Первое выражение - это формула для вычисления площади конической поверхности Sb. Второе выражение знакомо каждому школьнику, это формула для определения длины окружности L.
Выражаем радиус r из второго выражения, подставляем его в первое:
r = L / (2 × pi);
Sb = pi × L / (2 × pi) × s
Тогда искомая формула длины образующей конуса примет вид:
s = 2 × Sb / L
Подставляем данные площади Sb и длины L в эту формулу, получаем ответ: s = 8 см.
Задача с площадью основания и высотой
Известно, что круглое основание конуса имеет площадь 40 см2. Высота фигуры в 2 раза больше диаметра этого основания. Необходимо найти длину генератрисы конуса.
Как и в предыдущем случае, запишем два уравнения, опираясь на условие задачи:
So = pi × r2;
h = 4 × r
Первая формула - это известное выражение для площади круга. Второе равенство следует из того факта, что высота больше в 2 раза диаметра, а значит, в 4 раза радиуса r.
Оба выражения позволяют через So выразить r и h:
r = √(So / pi);
h = 4 × √(So / pi)
Теперь воспользуемся формулой образующей конуса через h и r. Получаем:
s = √(So / pi + 16 × So / pi) = √(17 × So / pi)
Подставляем величину So в равенство и записываем ответ: s ≈ 14,72 см.
