Круглый конус в геометрии является симметричной пространственной фигурой, имеющей ось вращения. Одной из важных его характеристик является площадь сечения осевого. В данной статье приведем формулу площади сечения осевого конуса прямого с круглым основанием и усеченного.
О какой фигуре будет идти речь?
Круглый конус - это фигура, которую можно получить следующим образом. Необходимо взять треугольник с углом прямым и его вокруг одного из катетов вращать. Тогда получится показанная ниже объемная фигура.
 Вам будет интересно:Правила английского языка: формы глагола send
Вам будет интересно:Правила английского языка: формы глагола send
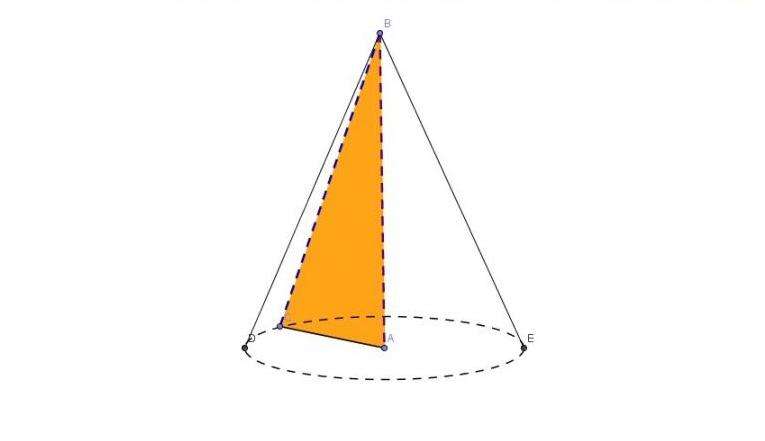
Отрезок AC на рисунке называется радиусом основания, который "рисует" при вращении с центром в точке A круг. Катет AB - это высота конуса. Очевидно, что отрезок AB перпендикулярен основанию и является частью оси вращения фигуры. Точка B - это высота рассматриваемой фигуры. Отрезок BE называется образующей, или генератрисой конуса. Совокупность всех генератрис образует боковую поверхность конуса. Она является конической. Ограничивающая основание окружность называется направляющей, или директрисой конуса.
Поскольку генератриса, радиус и высота являются гипотенузой и катетами рассмотренного прямоугольного треугольника, то для них можно записать формулу:
g2 = r2 + h2
Здесь g - генератриса, r - радиус, h - высота.
Осевое сечение конуса и его площадь
Чтобы записать для конуса формулу площади сечения осевого, сначала следует познакомиться с самим сечением. Оно получается так: нужно взять секущую плоскость, расположить ее параллельно оси конуса. Затем необходимо разрезать конус плоскостью на две одинаковые части таким образом, чтобы в плоскость сечения попала вершина фигуры.
Несложно себе представить, что в результате описанной операции получится равнобедренный треугольник. Равные стороны треугольника будут такие же, как длины генератрис. А третья сторона будет равна диаметру основания.

Формула площади осевого сечения конуса (фото см. выше) не отличается сложностью. Она соответствует формуле расчета этой величины для описанного треугольника. Поскольку у треугольника площадь равна произведению основания на высоту, которое следует поделить пополам, то искомое равенство для осевого сечения примет вид:
S = h*r
Эта формула говорит о том, что S в два раза больше площади прямоугольного треугольника, вращением которого был получен конус.
Усеченный конус и его осевое сечение
Усеченный конус получается из обычного при помощи секущей плоскости, которая параллельна его основанию. Полученная при этом фигура под плоскостью будет усеченным конусом. Он показан на рисунке.
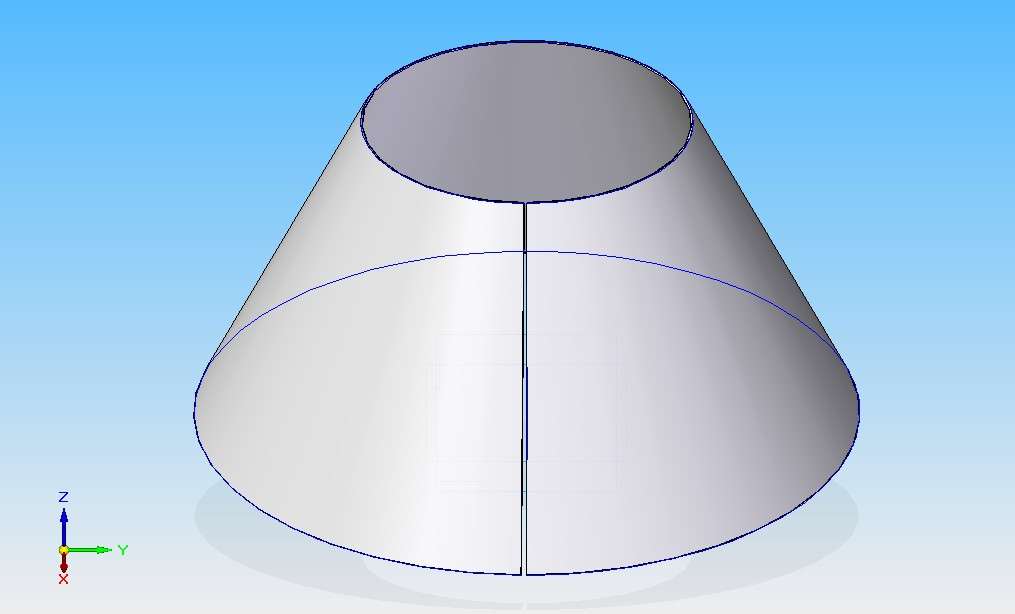
Помимо боковой поверхности, эта фигура состоит из двух оснований, которые представляют собой большой и малый круги. Обозначим их радиусы как r1 и r2. Расстояние между основаниями называется высотой, обозначим ее буквой h.
Осевое сечение рассматриваемого конуса будет четырехугольником, две стороны которого являются образующими. А две другие стороны будут параллельны друг другу и равны 2*r1 и 2*r2 соответственно. Этот четырехугольник будет равнобедренной трапецией, которая показана на рисунке ниже.
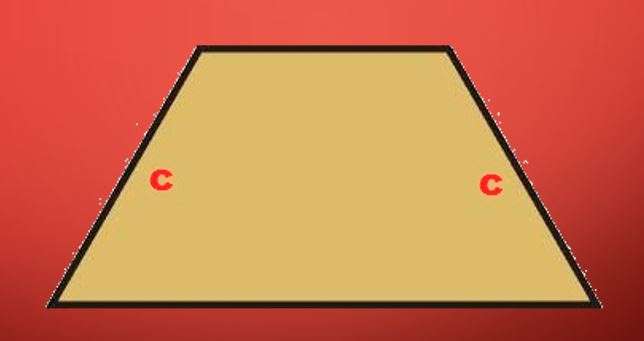
Этот факт позволяет использовать выражение для трапеции, чтобы записать формулу площади сечения усеченного осевого конуса . Она примет вид:
S = (2*r1 + 2*r2)/2*h = h*(r1 + r2)
То есть площадь S равна произведению суммы радиусов оснований усеченного конуса на его высоту.
Для решения геометрических задач также может потребоваться формула связи между генератрисой фигуры и ее параметрами r1, r2 и h. Соответствующее выражение приобретает вид:
g2 = h2 + (r1 - r2)2
Получить ее достаточно просто самостоятельно, если рассмотреть прямоугольный треугольник внутри конуса, построенный на сторонах g, h и (r1 - r2).
Задача на определение площади сечения осевого конуса усеченного
Покажем, как находить площадь осевого сечения на примере усеченного конуса.
Известно, что высота указанной фигуры составляет 10 см. Также известно, что для конуса осевого сечения площадь равна разности площадей оснований. Зная, что диаметры оснований отличаются ровно в два раза, необходимо найти площадь этого сечения по оси.
В соответствии с условием задачи можно записать два уравнения:
r1 = 2*r2;
h*(r1 + r2) = pi*(r12 - r22)
Значение высоты известно из условия. Таким образом, мы имеем 2 равенства и 2 неизвестные величины. Решаем эту систему:
h*(2*r2 + r2) = pi*((2*r2) 2 - r22) =>
3*pi*r22 - 3*h*r2 = 0
Мы получили неполное квадратное уравнение, которое следует решить относительно переменной r2. Уравнение имеет 2 корня, но решение r2 = 0 не является физическим, поэтому запишем только одно единственное значение для малого радиуса:
r2 = h/pi
Тогда большой радиус r1 будет равен:
r1 = 2*h/pi
Подставляя эти равенства в формулу площади осевого сечения конуса, получаем:
S = h*(r1 + r2) = 3*h2/pi
Подставляем численное значение h и записываем ответ: S ≈ 95,54 см2.
