Цилиндр и конус являются фигурами вращения, которые получаются в результате перемещения образующей вдоль направляющей линии. В данной статье раскроем вопрос, что это - образующая конуса, а также покажем, как рассчитывать ее длину в случае обычного конуса и его усеченного варианта.
Фигура конус общего типа
Речь идет о геометрической объемной фигуре, которая получается следующим образом: представим, что имеется некоторая кривая на плоскости, например, эллипс. Выберем в пространстве совершенно любую точку, которая не лежит в плоскости эллипса. Теперь с помощью прямого отрезка соединим точку и эллипс, а затем будем перемещать этот отрезок вдоль эллиптической кривой. Результатом такого перемещения будет коническая поверхность. Она показана ниже на рисунке.
 Вам будет интересно:Методическая деятельность: основные принципы, назначение, функции, методы и рекомендации по организации
Вам будет интересно:Методическая деятельность: основные принципы, назначение, функции, методы и рекомендации по организации
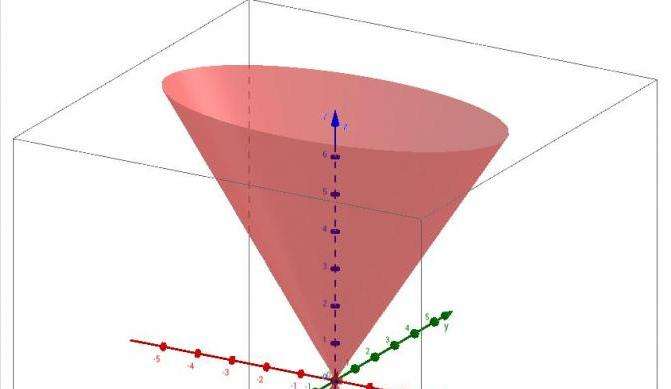
Здесь лежащая в начале координат точка называется вершиной конуса. Эллиптическая кривая - это направляющая или директриса фигуры. Образующая конуса - это отрезок, который соединяет его вершину с любой точкой направляющей кривой. Образующая также называется генератрисой. Из рисунка понятно, что длина образующей изменяется при ее движении вдоль эллипса.
Конус круглый
Круглым называется любой конус, направляющая кривая которого является окружностью. Если перпендикуляр, который проведен из вершины этого конуса, пересекает круглое основание в центре, то такая фигура будет называться прямой. Круглый прямой конус приведен на рисунке.
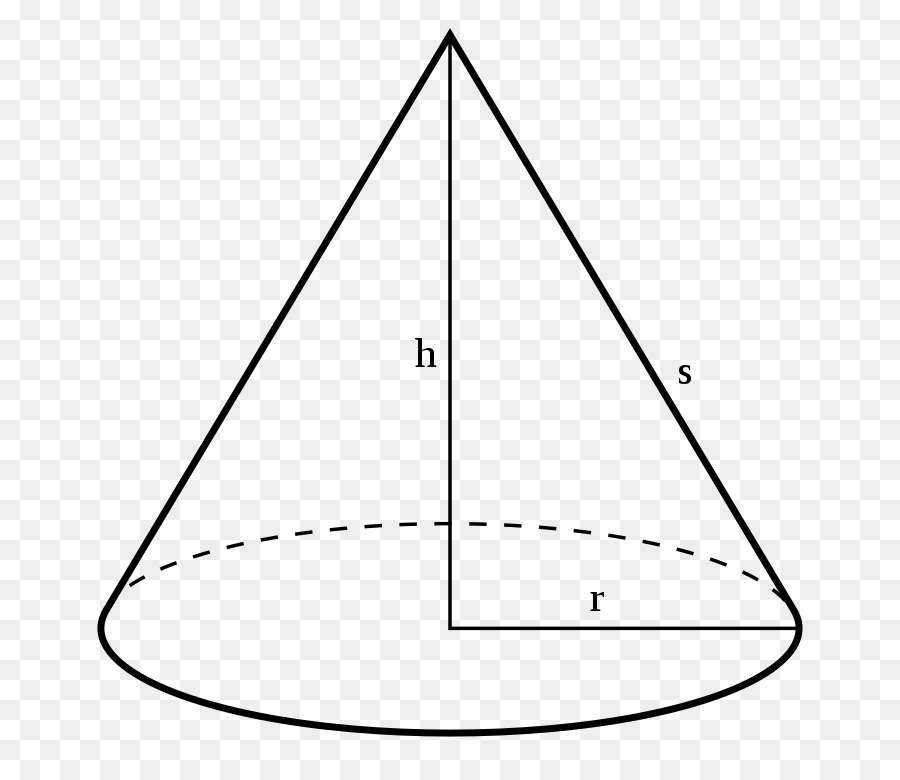
Рисунок ясно показывает, что для этой фигуры высота h, любой радиус r и образующая s составляют прямоугольный треугольник. Используя абстрактное воображение, можно представить, что если этот треугольник вращать вокруг h, то получится круглый конус.
Образующая конуса - это гипотенуза описанного прямоугольного треугольника. Этот факт позволяет записать равенство, которое можно использовать при вычислении длины образующей s:
s = √(r2+h2)
Отметим, что в отличие от конуса общего типа, все длины образующих для круглой фигуры равны между собой и составляют с основанием определенный угол. Если обозначить этот угол буквой φ, то можно записать еще две формулы для определения длины s:
s = r/cos(φ);
s = h/sin(φ).
Конус круглый усеченный
Предположим, что у нас имеется трапеция с двумя прямыми углами. Если вращать ее вокруг стороны, прилегающей к этим углам, то получится усеченный конус.
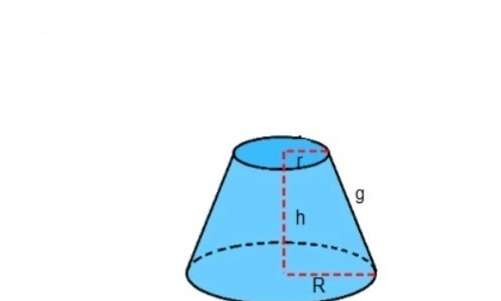
Рисунок показывает штриховыми линиями трапецию. Здесь r и R - радиусы малого и большого оснований, h - высота, g - это образующая конуса усеченного. Из рисунка видно, что все образующие для этой фигуры являются одинаковыми. Для определения длины g можно записать следующие три формулы:
g = √((R-r)2 + h2);
g = h/sin(φ);
g = (R-r)/cos(φ).
Здесь угол φ соответствует углу между образующей и большим основанием.
Заметим, что усеченный конус можно получить из обычного конуса, если отсечь плоскостью, которая параллельна его основанию, верхнюю часть фигуры.
Задача на определение генератрисы конуса усеченного
Решим интересную геометрическую задачу. Предположим, что имеется круглый конус усеченный. Известно, что высота этой фигуры равна 14 см, а угол между его образующей и малым основанием составляет 135o. Необходимо найти длину образующей конуса.
Если бы был дан угол между образующей и большим основанием, то мы сразу могли применить соответствующую формулу для вычисления g. Тем не менее, этот угол φ определить несложно.
Обратимся к предыдущему рисунку. Известен угол между r и g. Если переместить высоту h вдоль радиуса r к его концу, тогда стороны h, R-r и g образуют прямоугольный треугольник. Поскольку между h и r угол равен 90o, то между h и g он составит:
α = 135o - 90o = 45o.
Это означает, что угол φ будет также равен 45o, поскольку он является углом прямоугольного треугольника, упомянутого выше.
Для определения длины образующей g следует подставить известные данные в формулу. Получаем:
g = h/sin(φ) = 14/sin(45o) ≈ 19,8 см.
Для любого конуса длина его образующей больше высоты.
