Вычисление площадей фигур в пространстве и на плоскости является одной из приоритетных задач геометрии, которая имеет практическое применение. Для расчета площадей используют формулы, математический вид которых определяется формой рассматриваемой фигуры. В данной статье приведем формулы площади боковой поверхности конуса обычного и усеченного.
Конус как геометрическая фигура
Конусом в общем случае называется фигура, которая образована конической поверхностью и основанием. Начертить ее можно следующим способом: предположим, что имеется некоторая плавная плоская кривая (окружность, парабола и так далее), если соединить все точки этой кривой с некоторой единственной точкой пространства, то можно получить коническую поверхность.
 Вам будет интересно:Арка Тита в Риме: история, описание, фото
Вам будет интересно:Арка Тита в Риме: история, описание, фото
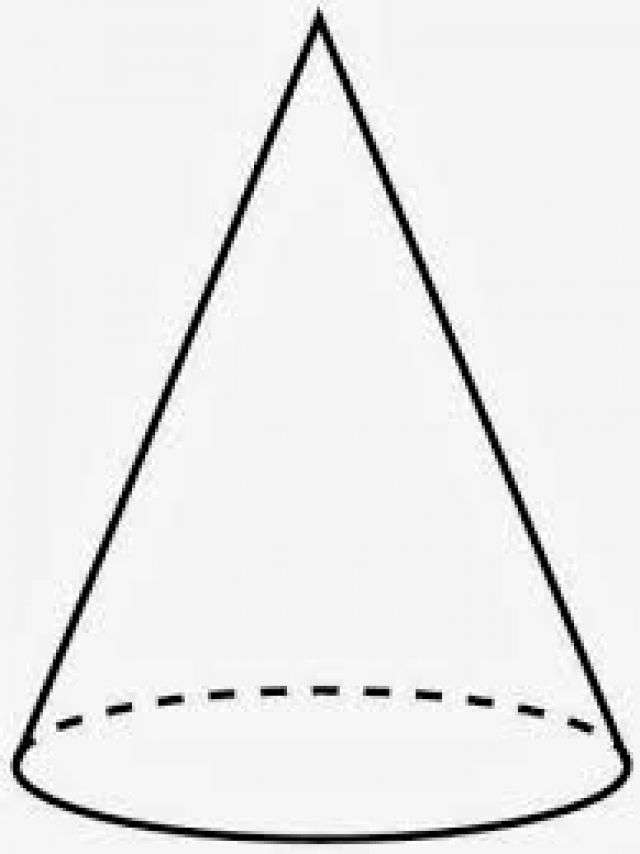
В большинстве случаев на практике и при решении задач по стереометрии рассматривают конкретный вид конуса - прямую фигуру с круглым основанием. По его названию понятно, что кривой, на которую коническая поверхность опирается, является окружность. Если из вершины конической поверхности опустить на основание перпендикуляр, то он пересечет его в центре круга. Это достаточный признак, чтобы считать конус прямым. Описанная фигура показана ниже на рисунке.
Круглый конус: площадь боковой поверхности
Формулу для площади поверхности боковой рассматриваемой фигуры можно получить, если разобраться, о чем идет речь. Как выше уже было сказано, любой конус состоит из двух частей:
- основание;
- коническая поверхность.
Вопрос нахождения площади основания сводится к расчету этой величины для круга. Для конической же поверхности, которая является боковой для фигуры, решение поставленной задачи не является тривиальным.
Как найти площадь боковой поверхности конуса? Формулу можно записать, если развернуть на плоскость рассматриваемую поверхность. Делается это просто: коническая поверхность разрезается вдоль генератрисы (отрезок, соединяющий вершину и границу основания фигуры) и разворачивается. Результат этих действий приведен на рисунке.
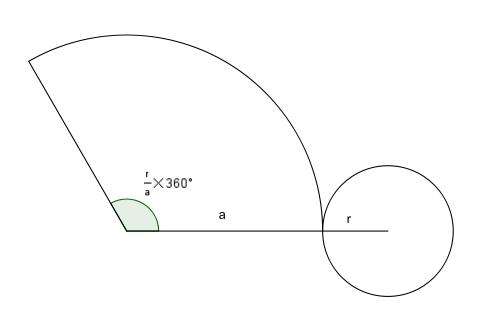
Видно, что коническая поверхность развернулась в круговой плоский сектор. На рисунке показан угол этого сектора в градусах. Он определяется отношением радиуса r круга, находящегося в основании, и генератрисы a. Не вдаваясь в математические вычисления, запишем формулу площади поверхности боковой конуса:
S = pi*r*a.
То есть искомая площадь зависит от двух параметров: длины радиуса и генератрисы.
Боковая поверхность конуса усеченного
Теперь приведем формулу площади боковой поверхности усеченного конуса. Эта фигура получается, если верхнюю часть обычного конуса отрезать плоскостью, при этом режущая плоскость должна быть параллельна круглому основанию. Фигура при этом будет образована уже двумя основаниями и одной поверхностью боковой.
Для определения площади поверхности боковой проделаем те же самые операции по получению развертки фигуры, что в случае с обычным конусом. Получим следующую картину.
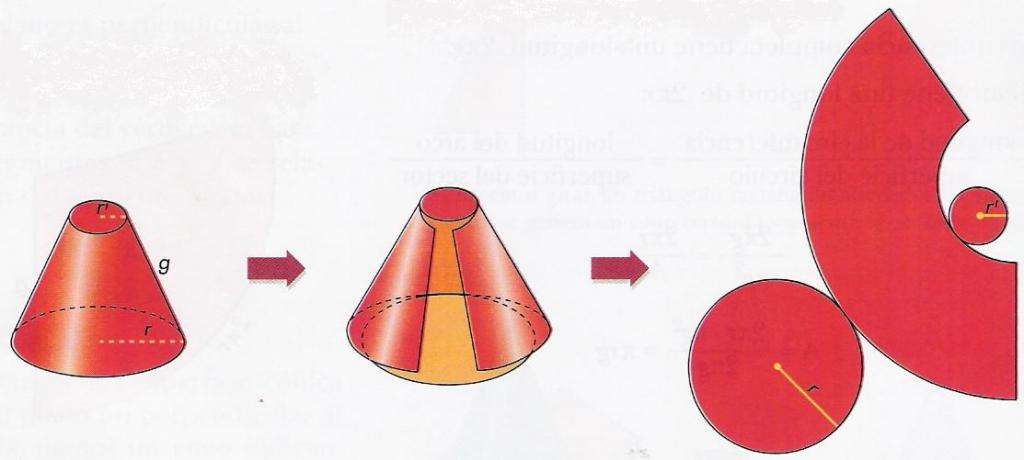
Боковая поверхность представлена круговым сектором, у которого вырезан центр. Формула для его площади имеет вид:
S = pi*g*(r + r').
Соответствующие величины обозначены на рисунке.
Задача на определения площади обычного конуса
Известно, что круглый конус имеет радиус 10 см и высоту 12 см. Необходимо найти полную площадь его поверхности.
Искомая площадь имеет две составляющие. Для основания эта величина составит:
So = pi*r² = 3,14*10² = 314 см².
Перед расчетом боковой поверхности следует вычислить длину генератрисы a фигуры. Рассматривая соответствующий прямоугольный треугольник, можно записать равенство:
a = √(r² + h²) = √(10² + 12²) = 15,62 см.
Теперь можно воспользоваться записанной формулой для площади поверхности конической:
Sb = pi*r*a = 3,14*10*15,62 ≈ 490,47 см².
Полную площадь фигуры находят сложением величин So и Sb. Выполняя указанное действие, получаем ответ: S ≈ 804,5 см².