Пространственные фигуры подробно рассматриваются в старших классах общеобразовательных школ в курсе стереометрии. Данная статья содержит ответ на вопрос о том, как найти образующую конуса круглого прямого и образующую соответствующей усеченной фигуры.
Фигура конус
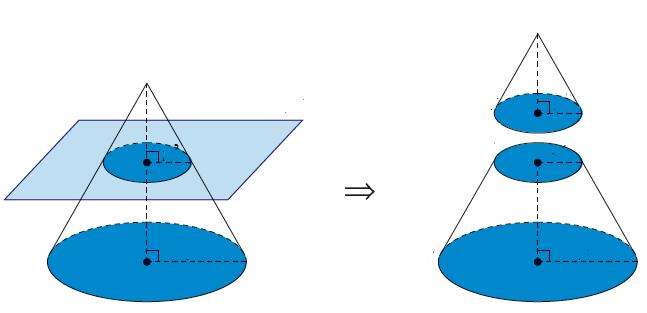
Чтобы понять, как найти образующую конуса, следует дать представление об этой фигуре. Круглым прямым конусом называют фигуру вращения прямоугольного треугольника вокруг одного из его катетов. Рисунок ниже демонстрирует процесс вращения.
 Вам будет интересно:Что значит: «Лучшее - враг хорошего», или Как избежать несчастного случая
Вам будет интересно:Что значит: «Лучшее - враг хорошего», или Как избежать несчастного случая
Полученная пространственная фигура имеет следующие характеристики:
Заметим, что высота фигуры пересекает круглое основание в его центре. Это является достаточным условием, чтобы считать конус прямым.
Образующая конуса
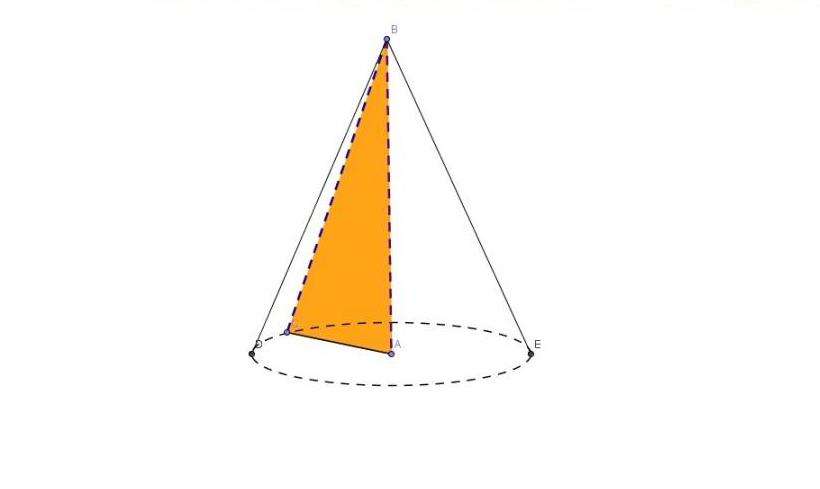
Теперь можно переходить к ответу на вопрос о том, как найти образующую конуса круглого прямого. Выше было сказано, что она представляет собой отрезок, который лежит на конической поверхности и соединяет вершину с точкой окружности основания. В прямоугольном треугольнике, из которого был конус получен, образующая является гипотенузой. Это наблюдение позволяет записать известную теорему Пифагора, связав образующую g с радиусом r и высотой h фигуры. Формула, как найти образующую конуса, имеет вид:
g = √(r2 + h2)
Помимо этой формулы, на практике вместо высоты или радиуса фигуры может быть известен угол φ между образующей и основанием. В этом случае генератрису g можно рассчитать с помощью следующих выражений:
g = h/sin(φ);
g = r/cos(φ)
Эти формулы следуют из свойств тригонометрических функций синуса и косинуса.
Таким образом, вычисление образующей конуса возможно, если знать любые два параметра фигуры.
Фигура конус усеченный
Он также является фигурой вращения, только вместо прямоугольного треугольника следует вращать прямоугольную трапецию. На рисунке ниже показан усеченный конус.
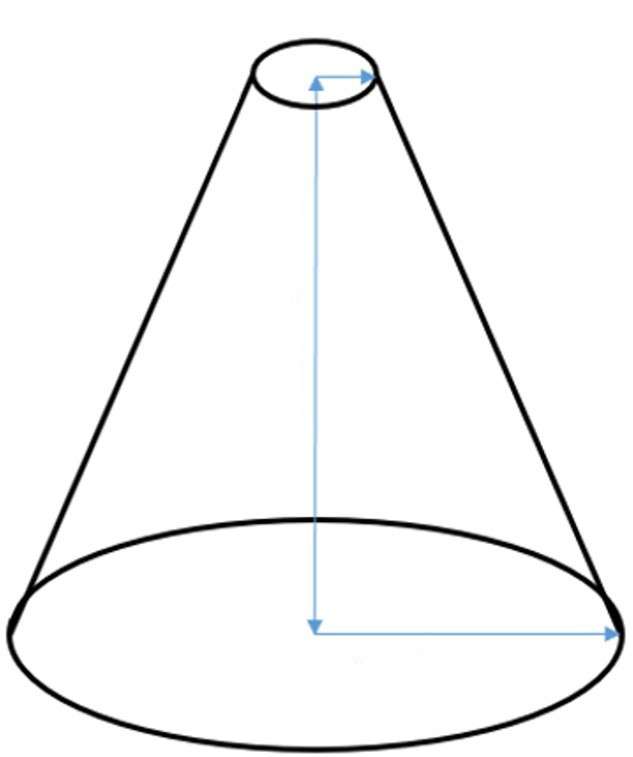
Здесь синие стрелки показывают прямоугольную трапецию. Длина вертикальной стрелки является высотой h фигуры, длины двух других синих стрелок - это радиусы оснований конуса. В отличие от цилиндра, основания усеченного конуса имеют разную площадь. Обозначим их радиусы r1 и r2. Четвертая наклонная к основанию сторона трапеции является образующей или генератрисой. Как и для обычного конуса, для усеченного все генератрисы равны друг другу и образуют боковую поверхность фигуры.
Заметим, что усеченный конус получил такое название потому, что его можно получить не только вращением трапеции, но и с помощью отсечения плоскостью верхней части круглого прямого конуса.
Генератриса усеченной фигуры
Итак, мы познакомились с усеченным конусом, а также с понятием о его образующей. Как находить образующую конуса усеченного? Для того чтобы получить нужную формулу, заметим, если высоту h перенести параллельно самой себе к боковой поверхности конуса так, чтобы она касалась одним концом образующей фигуры, то получится прямоугольный треугольник. Его сторонами будут высота h (катет), генератриса g (гипотенуза) и r1-r2 (катет). Тогда можно записать формулу для определения g:
g = √((r1 - r2)2 + h2)
Соответственно, если дан острый угол φ1 между большим основанием и генератрисой, тогда последнюю можно определить так:
g = h/sin(φ1);
g = (r1 - r2)/cos(φ1)
Если же известен тупой угол φ2 между малым основанием и генератрисой, тогда для ее вычисления необходимо применять такие выражения:
g = h/sin(φ2);
g = (r2 - r1)/cos(φ2)
Здесь первая формула является точно такой же, как для угла φ1, а во второй формуле радиусы в числителе поменялись местами.
Таким образом, найти образующую конуса усеченного можно, если знать любые три его параметра.