Рассмотрение свойств объемных фигур является одной из приоритетных задач геометрии. Важными характеристиками всех пространственных фигур являются объем и площадь поверхности. В статье раскрывается вопрос о том, что это — усеченный конус, и приводятся формулы для определения площади его поверхности и объема.
Фигура конус
Прежде чем отвечать на вопрос о том, что это — усеченный конус, необходимо познакомиться с фигурой, от которой он образован. Конусом в геометрии принято называть фигуру, получаемую с помощью соединения прямыми отрезками некоторой точки пространства со всеми точками заданной кривой. Точка пространства не должна лежать в плоскости кривой, она называется вершиной конуса. Соединяющие отрезки - это образующие фигуры, а плоская кривая - это направляющая. Она ограничивает основание конуса. В свою очередь, совокупность всех образующих называется конической поверхностью. Конус, основанием которого является круг, показан на рисунке.
 Вам будет интересно:Кем был Чингисхан по национальности?
Вам будет интересно:Кем был Чингисхан по национальности?
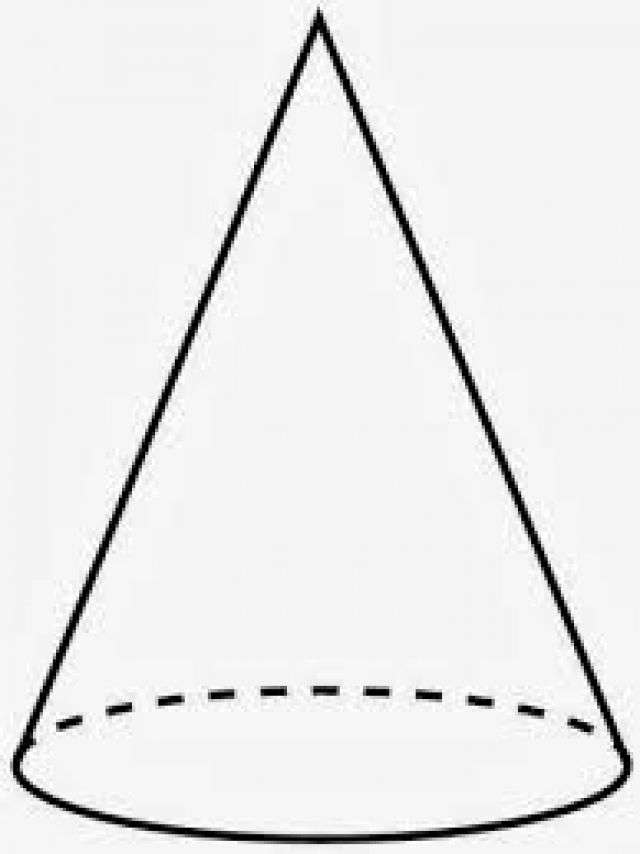
Расстояние между вершиной фигуры и основанием называется высотой. Если соответствующий перпендикуляр пересекает основание в геометрическом центре, то фигуру называют прямой.
 Вам будет интересно:«Земляк» – это соотечественник и поддержка на чужбине
Вам будет интересно:«Земляк» – это соотечественник и поддержка на чужбине
Дальше в статье покажем, как, используя прямой круглый конус, получить усеченную фигуру.
Усеченный конус и способы его получения
Предположим, что у нас имеется фигура, которая была показана в предыдущем пункте. Возьмем плоскость, параллельную основанию конуса, и отсечем с помощью нее вершину фигуры. Этот процесс показан на рисунке.
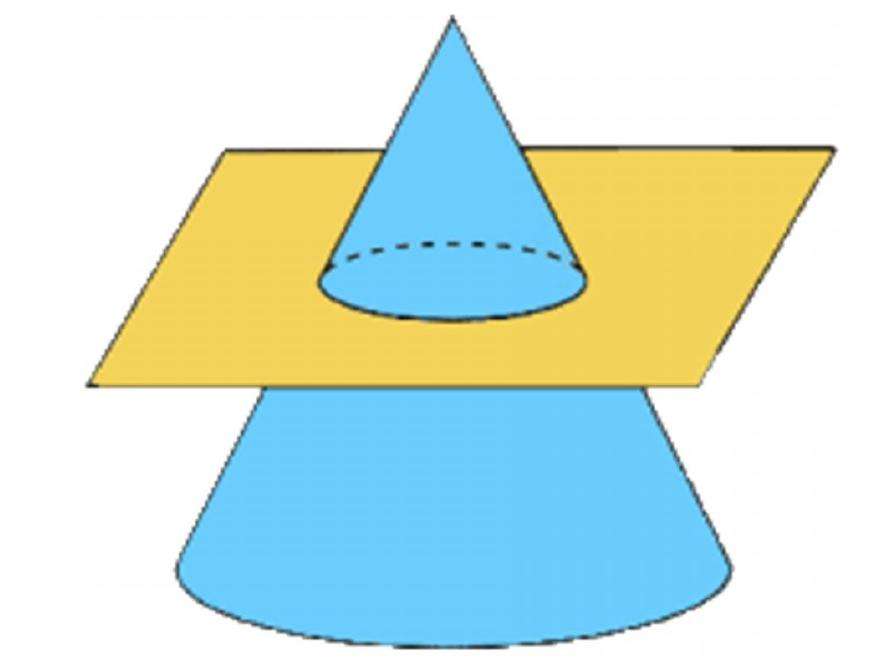
Образованная над плоскостью фигура является конусом, а вот фигура под плоскостью - это конус усеченный.
Существует еще один способ получения рассматриваемой фигуры. Предположим, что имеется некоторая трапеция с двумя прямыми углами. Если вращать эту трапецию вокруг стороны, к которой прямые углы прилегают, то она опишет поверхность усеченного конуса. Этот способ получения фигуры демонстрирует схема ниже.
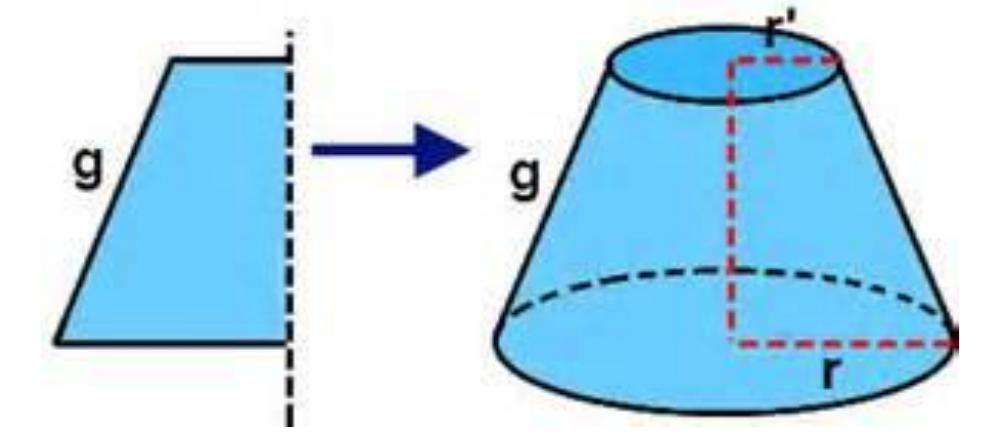
Сторона трапеции, вокруг которой выполнялось вращение, будет являться осью усеченного конуса. Отрезок, который на оси отсекают два основания фигуры, называется высотой. На рисунке отмечены образующая g и радиусы оснований конуса усеченного r и r'.
Наконец, третий способ получения усеченного конуса заключается в увеличении количества ребер усеченной пирамиды до бесконечного числа. Во время этого процесса пирамида постепенно перейдет в конус.
Любопытно отметить, что форма рассматриваемой геометрической фигуры в первом приближении в природе характерна для действующего вулкана, что отчетливо видно на следующей фотографии.
Элементы фигуры и ее линейные характеристики
Усеченный конус - это пространственная фигура, состоящая из трех поверхностей. Две из них представляют собой круглые основания (верхнее и нижнее) и одна - боковую поверхность. В отличие от многогранников, рассматриваемая фигура не имеет вершин и граней.
Важными параметрами конуса усеченного являются радиусы каждого из оснований. Будем больший радиус обозначать r1, меньший - r2. Помимо радиусов фигуры, для ее однозначного определения необходимо знать либо высоту h, либо образующую g. Указанные параметры связаны математически следующим равенством:
g2 = h2 + (r1 - r2)2
Все четыре параметра используются для определения площади поверхности и объема.
Поверхность усеченного конуса
Как отмечалось, состоит поверхность фигуры из трех частей. Если отрезать каждое из оснований от фигуры, а затем вдоль образующей разрезать и развернуть боковую поверхность, то мы получим развертку усеченного конуса. Рисунок ниже показывает, как она выглядит.
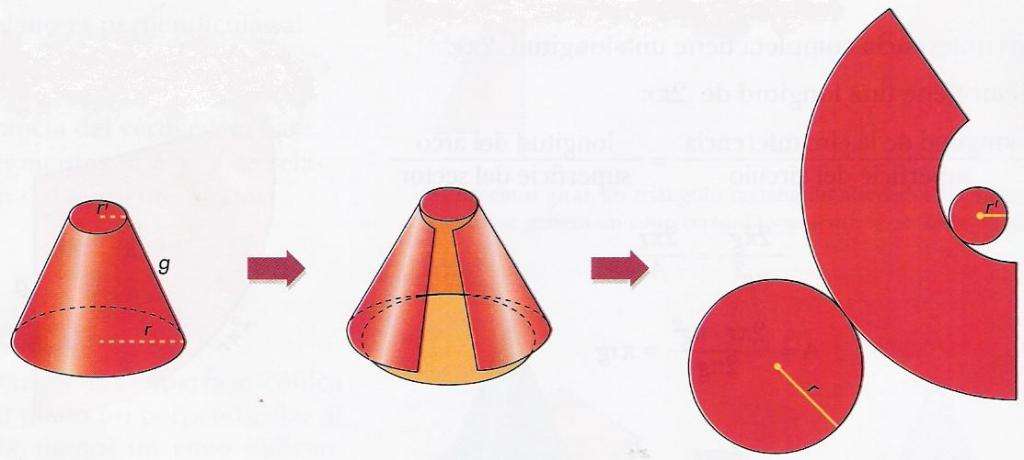
Площади оснований усеченного конуса находятся по простой формуле для соответствующей величины круга:
So1 = pi × r12;
So2 = pi × r22
С площадью боковой поверхности дело обстоит несколько сложнее. Можно заметить, что она представляет собой сектор круга, некоего радиуса G, у которого вырезали центральную часть радиусом G-g. Если это учесть, то можно получить формулу для площади боковой поверхности Sb. Здесь ограничимся лишь приведением конечного выражения:
Sb = pi × (r1 + r2) × g
Это выражение можно записать через радиусы и высоту h, однако тогда оно будет иметь несколько громоздкий вид.
Складывая записанные выражения, получаем формулу для определения площади S всей поверхности усеченного конуса:
S = So1 + So2 + Sb = pi × r12 + pi × r22 + pi × (r1 + r2) × g =
= pi × (r12 + r22 + (r1 + r2) × g)
Объем фигуры
Как и любая фигура в пространстве, усеченный конус тоже обладает некоторым объемом. Этот объем ограничен двумя основаниями и боковой поверхностью. Здесь не будем приводить подробный вывод соответствующей формулы для V. Запишем, как и в случае с площадью поверхности, лишь конечный результат:
V = h × pi / 3 × (r12 + r22 + r1 × r2)
Эта формула, в отличие от выражения для площади S, в качестве параметров содержит радиусы усеченного конуса и его высоту.
Далее в статье покажем, как следует использовать приведенные формулы для решения конкретной геометрической задачи.
Задача на определение площади и объема усеченного конуса
Ниже на рисунке изображен усеченный конус и приведены его линейные параметры. Необходимой найти площадь поверхности и объем фигуры.
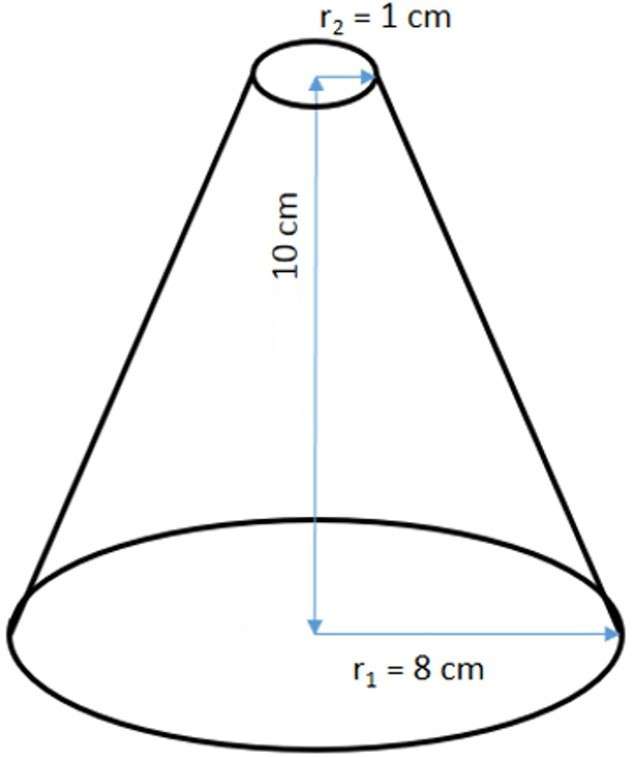
Начнем решать задачу с определения величины V. Ее вычисление не представляет никакого труда, поскольку известны все необходимые параметры. Подставляя их в формулу для V, получаем:
V = h × pi / 3 × (r12 + r22 + r1 × r2) =
= 10 × 3,14 / 3 × (82 + 12 + 8 × 1) ≈ 764,07 см3
Найденное значение соответствует 0,76 литра.
Чтобы найти площадь поверхности S, следует сначала вычислить длину образующей g фигуры. Она будет равна:
g = √(h2 + (r1 - r2)2) = √(102 + (8 - 1)2) ≈ 12,21 см
Значение образующей g мы округлили до сотых. Теперь можно воспользоваться формулой для площади S:
S = pi × (r12 + r22 + (r1 + r2) × g) = 3,14 × (82 + 12 + (8 + 1) × 12,21) ≈ 549,15 см2
Заметим, что формулы для V и S, которые мы использовали при решении задачи, справедливы только для круглого прямого усеченного конуса. В случае наклонной фигуры или же фигуры с некруглыми основаниями этими формулами пользоваться нельзя.

