Одним из самых распространенных видов перемещения объектов в пространстве, с которым человек встречается повседневно, является равноускоренное прямолинейное движение. В 9 классе общеобразовательных школ в курсе физики изучают подробно этот вид движения. Рассмотрим его в статье.
Кинематические характеристики движения
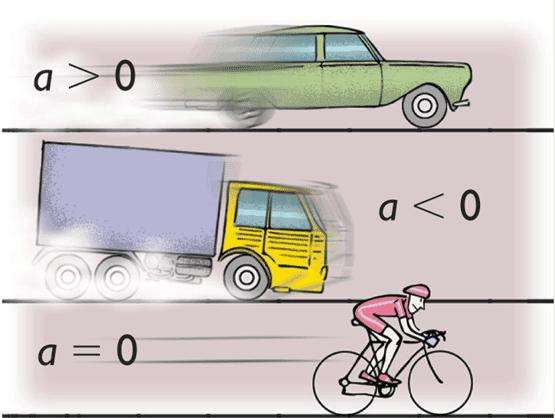
Прежде чем приводить формулы, описывающие равноускоренное прямолинейное движение в физике, рассмотрим величины, которые его характеризуют.
 Вам будет интересно:Значение цвета и таблица безопасных цветов
Вам будет интересно:Значение цвета и таблица безопасных цветов
В первую очередь это пройденный путь. Будем его обозначать буквой S. Согласно определению, путь - это расстояние, которое тело прошло вдоль траектории перемещения. В случае прямолинейного движения траектория представляет собой прямую линию. Соответственно, путь S - это длина прямого отрезка на этой линии. Он в системе физических единиц СИ измеряется в метрах (м).
Скорость или как часто ее называют линейная скорость - это быстрота изменения положения тела в пространстве вдоль его траектории перемещения. Обозначим скорость буквой v. Измеряется она в метрах в секунду (м/с).
 Вам будет интересно:Социалистические соревнования СССР: история возникновения, этапы проведения, победители
Вам будет интересно:Социалистические соревнования СССР: история возникновения, этапы проведения, победители
Ускорение - третья важная величина для описания прямолинейного равноускоренного движения. Она показывает, как быстро во времени изменяется скорость тела. Обозначают ускорение символом a и определяют его в метрах в квадратную секунду (м/с2).
Путь S и скорость v являются переменными характеристиками при прямолинейном равноускоренном движении. Ускорение же является величиной постоянной.
Связь скорости и ускорения
Представим себе, что некоторый автомобиль движется по прямой дороге, не меняя свою скорость v0. Это движение называется равномерным. В какой-то момент времени водитель стал давить на педаль газа, и автомобиль начал увеличивать свою скорость, приобретя ускорение a. Если начинать отсчет времени с момента, когда автомобиль приобрел ненулевое ускорение, тогда уравнение зависимости скорости от времени примет вид:
v = v0 + a * t.
Здесь второе слагаемое описывает прирост скорости за каждый промежуток времени. Поскольку v0 и a являются постоянными величинами, а v и t - это переменные параметры, то графиком функции v будет прямая, пересекающая ось ординат в точке (0; v0), и имеющая некоторый угол наклона к оси абсцисс (тангенс этого угла равен величине ускорения a).
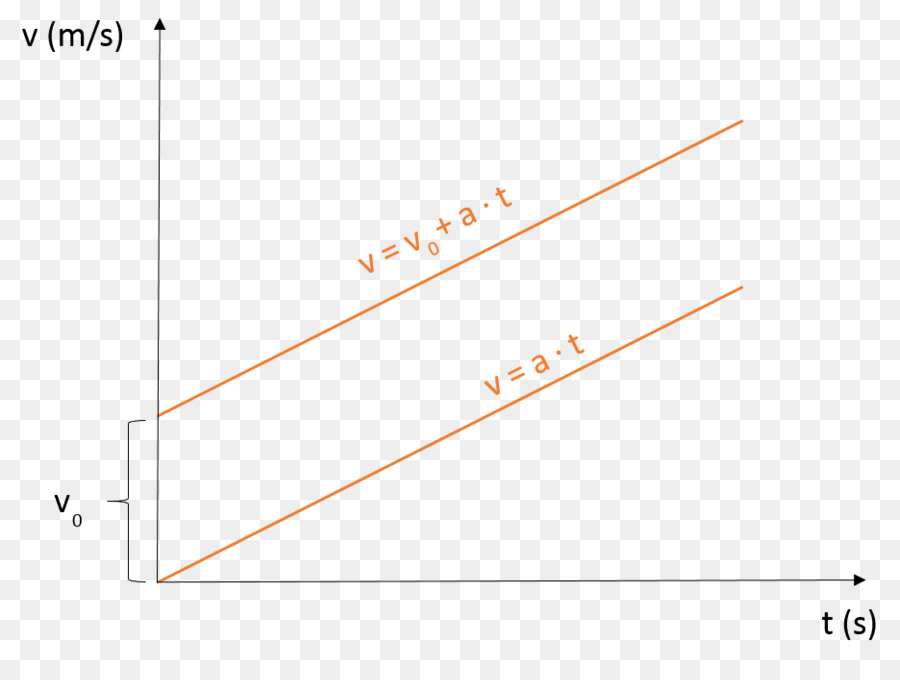
На рисунке показаны два графика. Отличие между ними заключается только в том, что верхний график соответствует скорости при наличии некоторого начального значения v0, а нижний описывает скорость равноускоренного прямолинейного движения, когда тело начало из состояния покоя ускоряться (например, стартующий автомобиль).

Отметим, если в примере выше водитель вместо педали газа нажал бы педаль тормоза, то движение торможения описывалось бы следующей формулой:
v = v0 - a * t.
Этот вид движения называется прямолинейным равнозамедленным.
Формулы пройденного пути
На практике часто важно знать не только ускорение, но и значение пути, который за данный период времени проходит тело. В случае прямолинейного равноускоренного движения эта формула имеет следующий общий вид:
S = v0 * t + a * t2 / 2.
Первый член соответствует равномерному движению без ускорения. Второй член - это вклад в пройденный путь чистого ускоренного движения.
В случае торможения движущегося объекта выражение для пути примет вид:
S = v0 * t - a * t2 / 2.
В отличие от предыдущего случая здесь ускорение направлено против скорости движения, что приводит к обращению в ноль последней через некоторое время после начала торможения.
Не сложно догадаться, что графиками функций S(t) будут ветви параболы. На рисунке ниже представлены эти графики в схематическом виде.
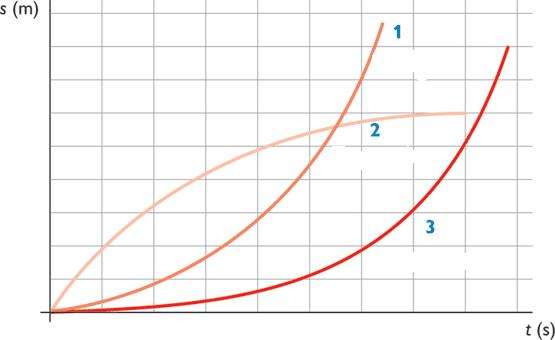
Параболы 1 и 3 соответствуют ускоренному перемещению тела, парабола 2 описывает процесс торможения. Видно, что пройденный путь для 1 и 3 постоянно увеличивается, в то время как для 2 он выходит на некоторую постоянную величину. Последнее означает, что тело прекратило свое движение.
Далее в статье решим три разные задачи на использование приведенных формул.
Задача на определение времени движения
Автомобиль должен отвести пассажира из пункта A в пункт B. Расстояние между ними 30 км. Известно, что авто в течение 20 секунд движется с ускорением 1 м/с2. Затем его скорость не меняется. За какое время авто доставит пассажира в пункт B?
Расстояние, которое авто за 20 секунд пройдет, будет равно:
S1 = a * t12 / 2.
При этом скорость, которую он наберет за 20 секунд, равна:
v = a * t1.
Тогда искомое время движения t можно вычислить по следующей формуле:
t = (S - S1) / v + t1 = (S - a * t12 / 2) / (a * t1) + t1.
Здесь S - расстояние между A и B.
Переведем все известные данные в систему СИ и подставим в записанное выражение. Получим ответ: t = 1510 секунд или приблизительно 25 минут.
Задача на расчет пути торможения
Теперь решим задачу на равнозамедленное движение. Предположим, что грузовой автомобиль двигался со скоростью 70 км/ч. Впереди водитель увидел красный сигнал светофора и начал останавливаться. Чему равен тормозной путь авто, если он остановился за 15 секунд.
Тормозной путь S можно рассчитать по следующей формуле:
S = v0 * t - a * t2 / 2.
Время торможения t и начальную скорость v0 мы знаем. Ускорение a можно найти из выражения для скорости, учитывая, что ее конечное значение равно нулю. Имеем:
v0 - a * t = 0;
a = v0 / t.
Подставляя полученное выражение в уравнение, приходим к конечной формуле для пути S:
S = v0 * t - v0 * t / 2 = v0 * t / 2.
Подставляем значения из условия и записываем ответ: S = 145,8 метра.
Задача на определение скорости при свободном падении
Пожалуй, самым распространенным в природе прямолинейным равноускоренным движением является свободное падение тел в поле гравитации планет. Решим следующую задачу: тело с высоты 30 метров отпустили. Какую скорость будет оно иметь в момент падения на поверхность земли?
Искомую скорость можно рассчитать по формуле:
v = g * t.
Где g = 9,81 м/с2.
Время падения тела определим из соответствующего выражения для пути S:
S = g * t2 / 2;
t = √(2 * S / g).
Подставляем время t в формулу для v, получаем:
v = g * √(2 * S / g) = √(2 * S * g).
Значение пройденного телом пути S известно из условия, подставляем его в равенство, получаем: v = 24,26 м/с или около 87 км/ч.
